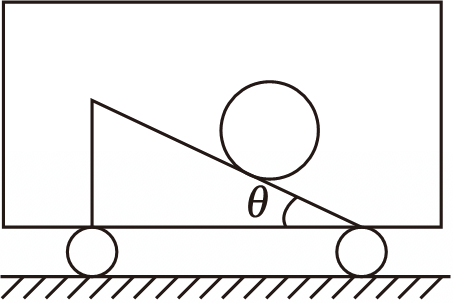
小车在水平面内运动，车内放置了一个可移动斜面体，斜面倾角为$\theta$，斜面体上表面光滑，下表面粗糙，与小车之间的动摩擦因数为$0.8$。将一光滑圆筒放在斜面体上，当小车以某一加速度做匀变速直线运动时，发现光滑圆筒、斜面体均与小车保持相对静止。斜面体质量与圆筒质量均为$2\;\rm kg$。最大静摩擦力等于滑动摩擦力，$g=10\;\rm m/s^{2}$，$\tan\theta=\dfrac{1}{2}$。下列说法中正确的是$(\qquad)$

小车的加速度为$5\\;\\rm m/s^{2}$，方向向右

小车的加速度为$8\\;\\rm m/s^{2}$，方向向右

斜面体与小车之间的摩擦力大小为$20\\;\\rm N$

斜面体与小车之间的摩擦力大小为$32\\;\\rm N$

$\rm AB$．对圆筒受力分析，结合平行四边形定则，可得其所受合力，如下图：

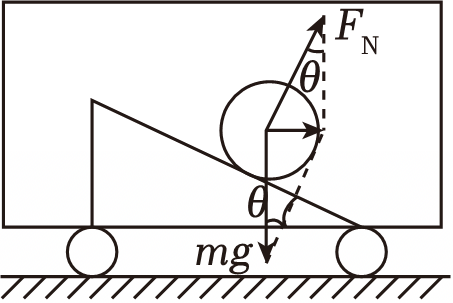
由牛顿第二定律可得：$mg\tan\theta=ma$，

解得：$a=5\;\rm m/s^{2}$，加速度方向向右，故$\rm A$正确，$\rm B$错误；

$\rm CD$．结合前面分析可知，光滑圆筒和斜面体这个整体的加速度为$a$，则该整体在水平方向上受到一个水平向右的静摩擦力，由牛顿第二定律可得：

$f=(M+m)a=(2+2)\times 5\;\rm N=20\;\rm N$，故$\rm C$正确，$\rm D$错误。

故选：$\rm AC$。