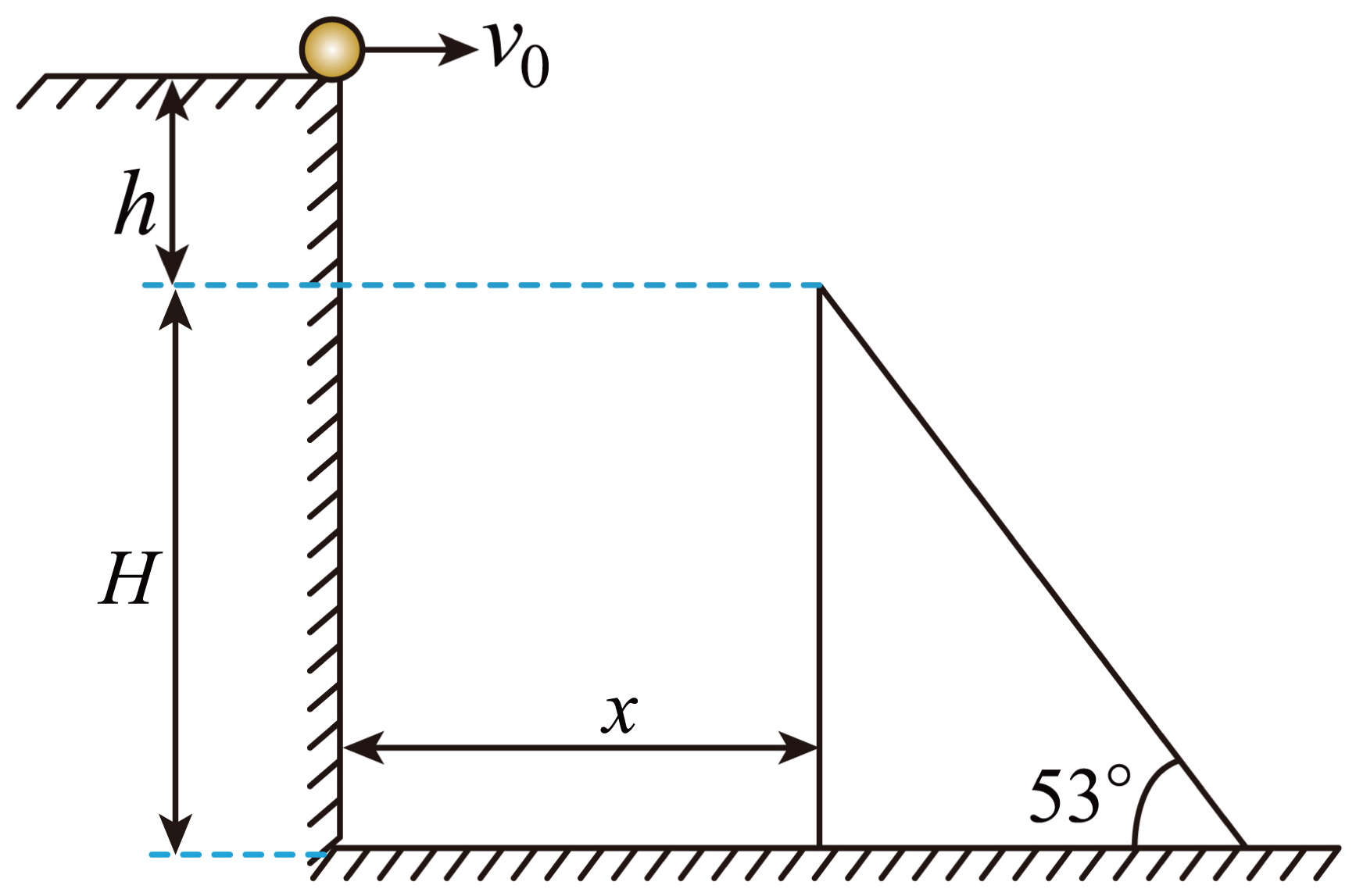
小球水平抛出的初速度$v_{0}$的大小，以及斜面顶端与平台边缘的水平距离$x$；

$v_{0}=3\\;\\rm m/s$，$x=1.2\\;\\rm m$

题意知小球恰好无碰撞地落在邻近平台并沿斜面下滑，可知小球的速度偏转角为$53^\circ $，由平抛运动规律有$h=\dfrac{1}{2}gt^{2}$，解得$t=0.4\;\rm s$，因为$\tan 53{^\circ}= \dfrac{gt}{v_{0}}$，联立解得$v_{0}=3\;\rm m/s$，则斜面顶端与平台边缘的水平距离$x=v_{0}t=1.2\;\rm m$

小球沿斜面运动的时间。

$1\\;\\rm s$

结合以上分析可知，小球落在斜面顶端时速度$v=\dfrac{v_{0}}{\cos 53{^\circ}}=5\;\rm m/s$

在斜面，对小球有$mg\sin 53^\circ-\mu mg\cos 53^\circ =ma$

解得加速度$a=5\;\rm m/s^{2}$

由运动学公式有$\dfrac{H}{\sin 53{^\circ}}=vt_{0}+\dfrac{1}{2}at_{0}^{2}$

代入题中数据，联立解得$t_{0}=1\;\rm s$