高中 | 闭合电路的欧姆定律基本问题 题目答案及解析
稿件来源:高途
高中 | 闭合电路的欧姆定律基本问题题目答案及解析如下,仅供参考!
选修3-1
第二章 恒定电流
2.7 闭合电路的欧姆定律
闭合电路的欧姆定律基本问题
热敏电阻的阻值随温度的变化而改变,通过建立温度与热敏电阻两端电压的关系,可制作一简易的温度传感器,进而实现温度测量。如图($a$)所示,$R_{T}$为热敏电阻,$R_{0}$为匹配电阻,电源电动势为$E$(内阻不计),数字电压表$\rm V$(内阻视为无穷大)用于测量热敏电阻两端的电压$U_{out}$。
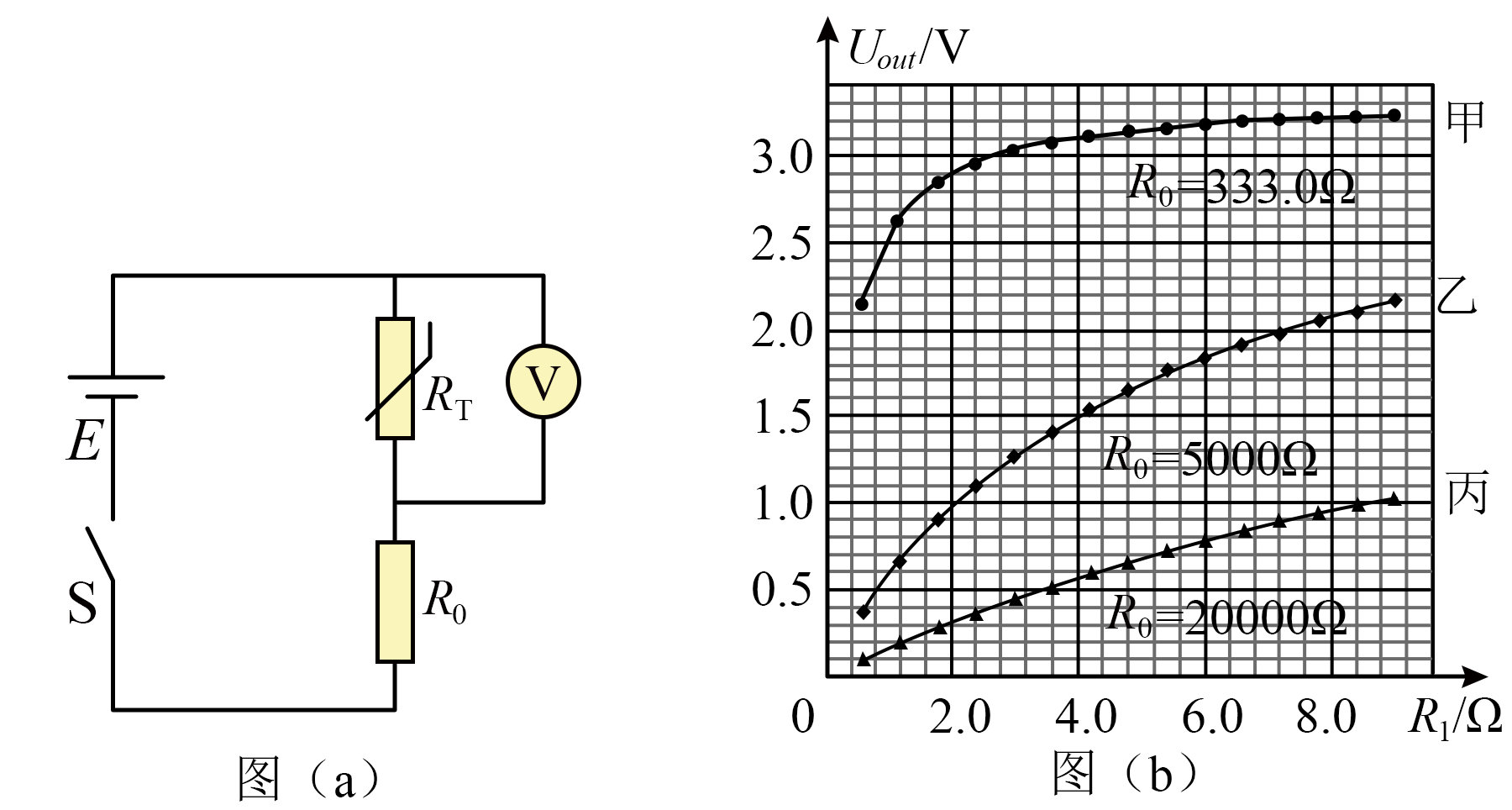
由图($a$)可得$U_{out}$的表达式为 。
由闭合电路的欧姆定律可得电路中电流$I=\dfrac{E}{R_{0}+R_{\text{T}}}$
可得$U_{out}=IR_{\text{T}}=\dfrac{R_{\text{T}}}{R_{\text{T}}+R_{0}}E$
已知某热敏电阻从$20^\circ\rm C$升温到$100^\circ\rm C$时,其阻值从$10\;\rm k\Omega$单调减小到$0.5\;\rm k\Omega$。为了合理配置$R_{0}$的阻值,用电阻箱$R_{1}$代替该热敏电阻$R_{T}$进行实验。经数据处理得到不同$R_{0}$值对应的$U_{out} − R_{1}$关系图线,如图($b$)所示,分析可知应选图线 对应的$R_{0}$作为匹配电阻,可使$U_{out}$在更宽范围内对$R_{1}$变化的响应更灵敏。
由图($b$)可知,图线乙在相同的$R_{1}$变化区间,$U_{out}$变化范围更大,即图线乙对应的$R_{0}$作为匹配电阻,可使$U_{out}$在更宽范围内对$R_{1}$变化的响应更灵敏。
①选定匹配电阻$R_{0}$后,按图($a$)连接电路,改变热敏电阻的温度$T$,测量其两端的电压$U_{out}$,并尝试用二次多项式进行数据拟合,得到温度$T(^\circ\rm C)$与$U_{out}(V)$的关系。
②用已标定的温度传感器进行实验,记录数据,如下表所示,其中$T$为测量温度,$T_{b}$为标准温度,$\Delta T=T − T_{b}$。表中绝对误差最大和最小的测量温度值$T$分别为 $^\circ\rm C$和 $^\circ\rm C$。除涉及元器件的精度和稳定性之外,分析该温度传感器测量误差的主要来源: 。
| $T(^\circ\rm C)$ | $29.6$ | $34.0$ | $38.0$ | $42.2$ | $47.0$ | $51.6$ | $55.0$ | $66.1$ | $70.2$ |
| $T_{b}(^\circ\rm C)$ | $31.4$ | $36.4$ | $40.5$ | $44.5$ | $48.7$ | $52.5$ | $55.8$ | $65.7$ | $70.0$ |
| $\Delta T(^\circ\rm C)$ | $-1.8$ | $-2.4$ | $-2.5$ | $-2.3$ | $-1.7$ | $-0.9$ | $-0.8$ | $0.4$ | $0.2$ |
结合表格数据分析,可知测量的绝对误差最大和最小对应的测量温度分别为$38.0^\circ\rm C$和$70.2^\circ\rm C$。
误差的主要来源除去涉及元器件的精度和稳定性之外,可能是匹配电阻$R_{0}$的阻值不太合适或选用二次多项式进行数据拟合不够精确。
高中 | 闭合电路的欧姆定律基本问题题目答案及解析(完整版)
