高中 | 机械能守恒定律 题目答案及解析
稿件来源:高途
高中 | 机械能守恒定律题目答案及解析如下,仅供参考!
必修2
第七章 机械能守恒定律
7.8 机械能守恒定律
机械能守恒定律
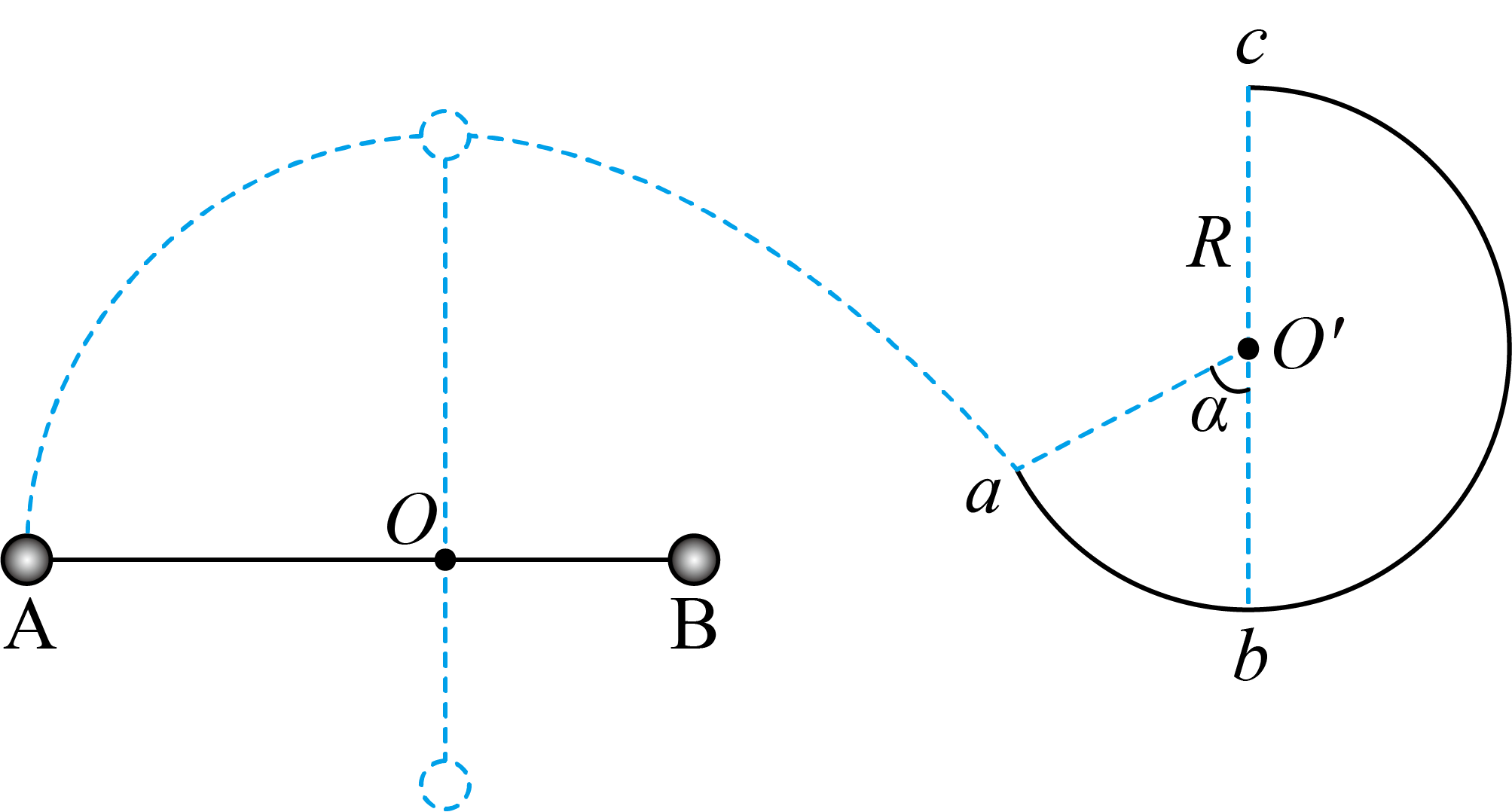
如图所示,质量不计的硬直杆可以绕光滑转轴$O$在竖直面内自由转动,杆两端分别固定质量$m=1\;\rm kg$的小球$A$和质量$M=4\;\rm kg$的小球$B$。已知小球$A$到$O$点的距离为$2\;\rm m$,小球$B$到$O$点的距离为$1\;\rm m$。现将杆从水平位置由静止释放,在杆转动到竖直位置时,小球$A$脱离杆水平飞出,恰能从$a$点无碰撞地进入与杆在同一竖直平面内的光滑圆弧轨道$abc$,到达圆弧轨道上$c$点之前的$d$点(图中未画出)脱离轨道。已知$b$为圆弧轨道的最低点,$c$为圆弧轨道的最高点,$O'$为圆弧轨道的圆心,$aO'$与竖直方向的夹角$\alpha=60^\circ$,不计空气阻力,取$g=10\;\rm m/s^{2}$。
杆转到竖直位置时,求杆对小球$B$的作用力;
$60\\;\\rm N$,方向竖直向上
"]]杆从水平位置由静止释放转动到竖直位置的过程,根据系统机械能守恒定律有$Mgl=mg \cdot 2l+ \dfrac{1}{2}mv_{\text{A}}^{\text{2}}+ \dfrac{1}{2}Mv_{\text{B}}^{\text{2}}$
由于两球具有相同的角速度,则$\dfrac{v_{\text{A}}}{v_{\text{B}}}=\dfrac{\omega \cdot 2l}{\omega l}=2$
代入数据解得$v_{\text{A}}=2\sqrt{5}\;\rm \text{m/s}$,$v_{\text{B}}=\sqrt{5}\;\rm \text{m/s}$
对小球$B$,根据牛顿第二定律有$F-Mg=M\dfrac{v_{\text{B}}^{\text{2}}}{l}$
解得$F=60\;\rm N$,方向竖直向上;
杆从水平位置转到竖直位置的过程中,求杆对小球$A$做的功;
$30\\;\\rm J$
"]]杆从水平位置转到竖直位置的过程中,对小球$A$,根据动能定理可得$W-mg \cdot 2l= \dfrac{1}{2}mv_{\text{A}}^{\text{2}}$
解得$W=30\;\rm J$
若$dO'$与竖直方向的夹角用$\theta$表示,写出$\cos\theta$与圆弧轨道半径$R$的关系式,并判断$R$的取值范围。
$\\cos\\theta=\\dfrac{8}{3R}- \\dfrac{1}{3}$,$2\\;{\\rm m}\\lt R\\lt 8\\;\\rm m$
"]]小球$A$脱离杆水平飞出,做平抛运动,到达$a$点时有$v_{a}=\dfrac{v_{\text{A}}}{\cos\alpha}= 4\sqrt{5}\;\rm \text{m/s}$
小球到达圆弧轨道上$c$点之前的$d$点脱离轨道,则$- mgR(\cos\alpha+\cos\theta)=\dfrac{1}{2}mv_{d}^{2}-\dfrac{1}{2}mv_{a}^{2}$
脱离轨道时有$mg\cos\theta=m\dfrac{v_{d}^{2}}{R}$
联立解得$\cos\theta=\dfrac{8}{3R}-\dfrac{1}{3}$
当小球恰好到达圆心等高处有$- mgR_{1}\cos\alpha=0-\dfrac{1}{2}mv_{a}^{2}$
解得$R_{1}=8\;\rm m$
当小球恰好到达$c$点有$- mgR_{2}(1+\cos\alpha)=\dfrac{1}{2}mv_{c}^{2}-\dfrac{1}{2}mv_{a}^{2}$
小球在$c$点,根据牛顿第二定律有$mg=m\dfrac{v_{c}^{2}}{R}$
解得$R_{2}=2\;\rm m$
所以要使得小球脱离轨道,则$R$的取值范围为$2\;{\rm m}\lt R\lt 8\;\rm m$。
高中 | 机械能守恒定律题目答案及解析(完整版)
