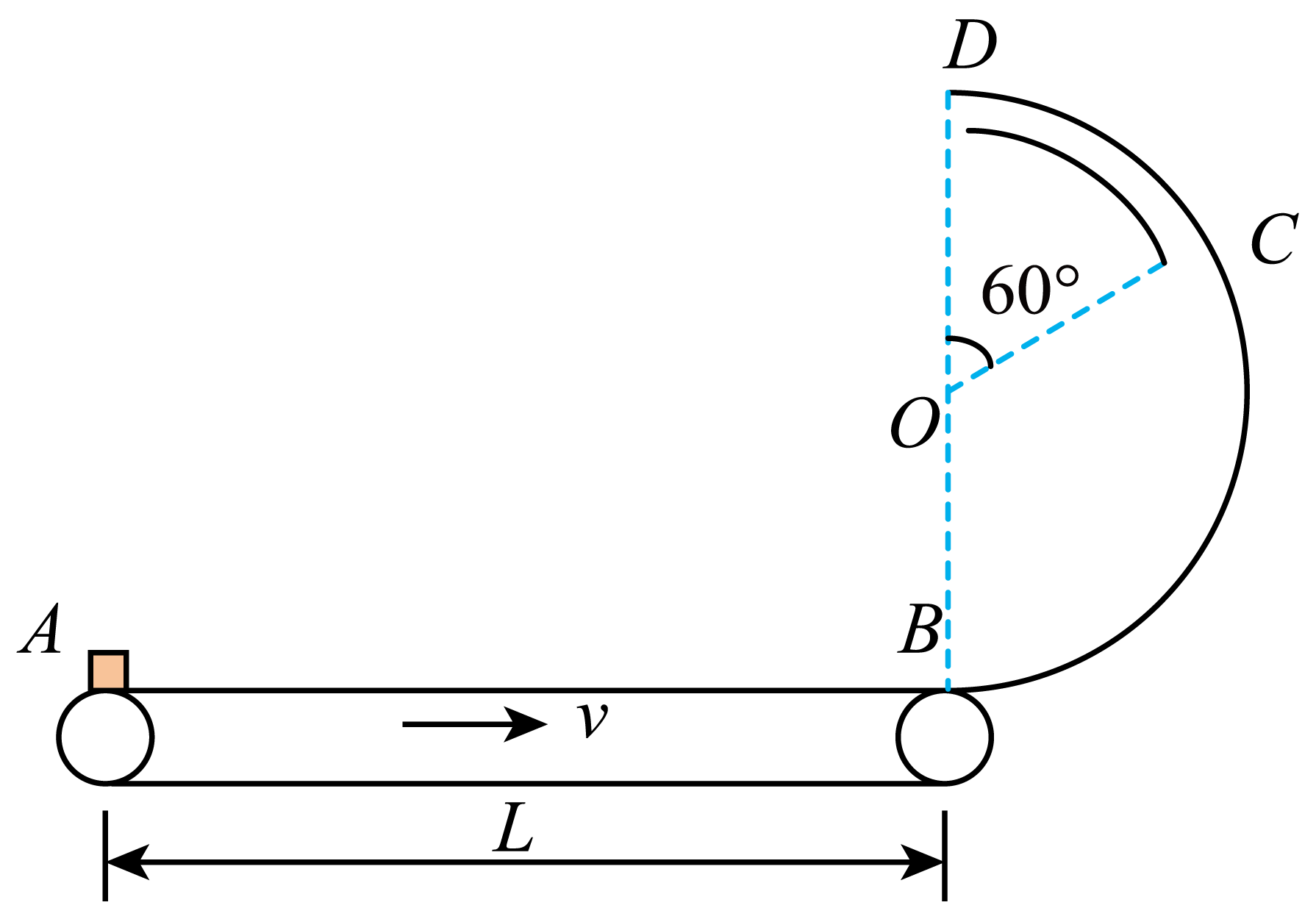
求小物块到达$B$点时的速度大小；

$4\\;\\rm m/s$

对小物块受力分析，由牛顿第二定律$\mu mg=ma$

解得$a=2\;\rm m/s^{2}$

设小物块与传送带共速的时间为$t_{1}$，由运动学公式$v=at_{1}$

可得$t_{1}=2\;\rm s$

加速的位移为$x_{1}=\dfrac{1}{2}at_{1}^{2}=4\;\rm \text{m}$

因为$4\;\rm \text{m}\lt \dfrac{25}{4}\ \text{m}$

所以小物块在传送带上先加速后匀速，到达$B$点时的速度大小为$4\;\rm m/s$。

求由于传送小物块，电动机多做的功；

$16\\;\\rm J$

小物块在传送带上因摩擦而产生的热量为$Q=\mu mg(vt_{1}-x_{1})=8\;\rm J$

由于传送小物块，电动机多做的功为$W_{额}=Q+\dfrac{1}{2}mv^{2}=8\;\rm \text{J}+\dfrac{1}{2} \times 1 \times 4^{2}\;\rm \text{J}=16\;\rm \text{J}$

若要使小物块从$D$点飞出后落回传送带的水平距离最大，求半圆轨道半径$R$的大小；

$0.2\\;\\rm m$

从$B$点到$D$点，由动能定理$- mg \cdot 2R=\dfrac{1}{2}mv_{D}^{2}-\dfrac{1}{2}mv^{2}$

小物块离开$D$点后做平抛运动，有$2R=\dfrac{1}{2}gt^{2}$

$x=v_{D}t$

联立可得$x=4\sqrt{- R^{2}+\dfrac{2}{5}R}=4\sqrt{- {\left(R-\dfrac{1}{5}\right)}^{2}+\dfrac{1}{25}}$

由数学关系可知，当$R=0.2\;\rm m$时，小物块从$D$点飞出后落回传送带的水平距离最大$x_{\max}=0.8\;\rm m$

若小物块在半圆轨道内运动时始终不脱离轨道且不从$D$点飞出，求半圆轨道半径$R$的取值范围。

$0.4\\;\\text{m} \\leqslant R \\leqslant \\dfrac{16}{35}\\text{m}$或$R\\geqslant 0.8\\;\\rm m$

①刚好沿半圆到达与圆心$O$等高处，根据动能定理$- mgR_{1}=0-\dfrac{1}{2}mv^{2}$

解得$R_{1}=0.8\;\rm m$

小物块在半圆轨道内运动时始终不脱离轨道，则$R\geqslant 0.8\;\rm m$

②刚好到达$C$点不脱轨，临界条件是弹力为$0$，在$C$点$mg\cos 60{^\circ}=m\dfrac{v_{C}^{2}}{R_{2}}$

从$B$点到$C$点，根据动能定理$- mgR_{2}(1+\cos 60{^\circ})=\dfrac{1}{2}mv_{C}^{2}-\dfrac{1}{2}mv^{2}$

代入数据解得$R_{2}=\dfrac{16}{35}\;\rm \text{m}$

③刚好到达$D$点不脱轨，在$D$点有$v_{0}=0$，从$B$点到$D$点，根据动能定理$- mg \cdot 2R_{3}=0-\dfrac{1}{2}mv^{2}$

代入数据解得$R_{3}=0.4\;\rm m$

若小物块在半圆轨道内运动时不从$D$点飞出，则满足$0.4\;\text{m} \leqslant R \leqslant \dfrac{16}{35}\;\rm \text{m}$

综上所述，半圆轨道半径$R$的取值范围为$0.4\;\text{m} \leqslant R \leqslant \dfrac{16}{35}\text{m}$或$R\geqslant 0.8\;\rm m$