光滑水平地面上，质量为$2\;\rm kg$、上表面粗糙的木板$B$正以$3\;\rm m/s$的速度向右运动。某时刻在木板右端滑上可视为质点的物块$A$，质量为$1\;\rm kg$，速度向左，大小也是$3\;\rm m/s$，物块和木板间的动摩擦因数为$0.2$，木板长为$7\;\rm m$。则下列说法正确的是$(\qquad)$

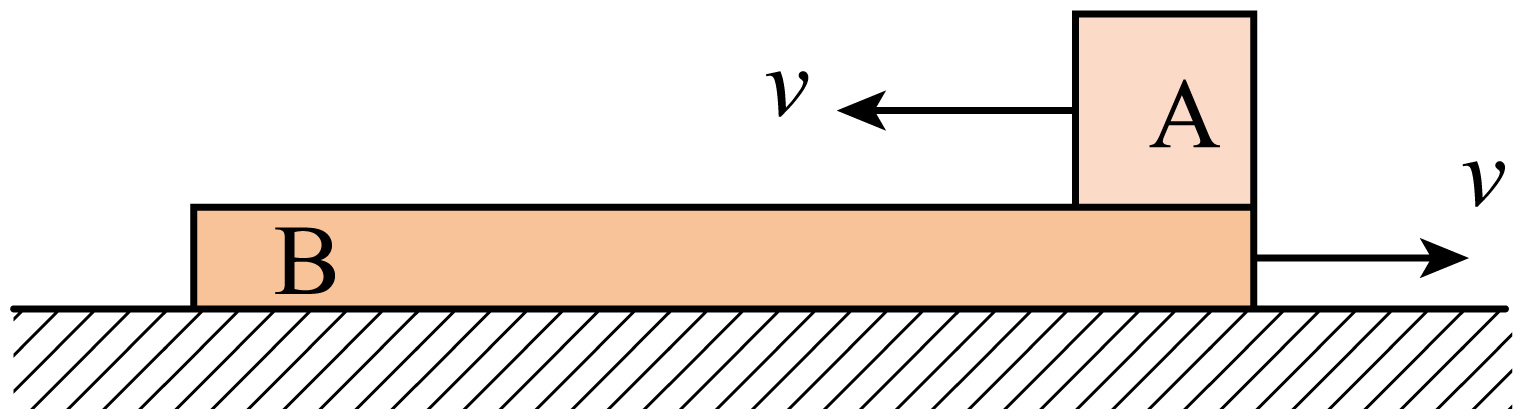
物块$A$从木板$B$的左端离开

经过$2\\;\\rm s$物块$A$与木板$B$相对静止

整个过程系统产生热量为$4\\;\\rm J$

相对静止后，物块$A$在木板$B$上移动的距离为$7m$

$\rm AD$．把$A$和$B$看成一个系统，该系统所受合力为零，所以$A$、$B$组成的系统满足动量守恒，设$A$没有从$B$上离开，最后的共同速度大小为$v'$，规定水平向右的方向为正方向，根据动量守恒定律有$m_{\rm B}v-m_{\rm A}v=(m_{\rm A}+m_{\rm B})v'$

$A$和$B$的相对位移的距离为$l$，根据能量守恒有$\dfrac{1}{2}m_{\text{A}}v^{2}+\dfrac{1}{2}m_{\text{B}}v^{2}=\dfrac{1}{2}\left( m_{\text{A}}+m_{\text{B}} \right)v'^{2}+\mu m_{\text{A}}gl$

代入数据解得$v'=1\;\rm m/s$，$l=6\;\rm m\lt 7\;\rm m$

假设成立，所以物块$A$没有从$B$的左端离开，故$\rm AD$错误；

$\rm B$．设$A$的加速度大小为$a$，根据牛顿第二定律有$\mu m_{\rm A}g=m_{\rm A}a$

设经过时间$t$，$A$与$B$保持相对静止，根据速度$—$时间关系有$v'=-v+at$

代入数据解得$t=2\;\rm s$

故$\rm B$正确；

$\rm C$．整个过程中系统产生的热量为$Q=\mu m_{\rm A}gl$

代入数据解得$Q=12\;\rm J$

故$\rm C$错误。

故选：$\rm B$。