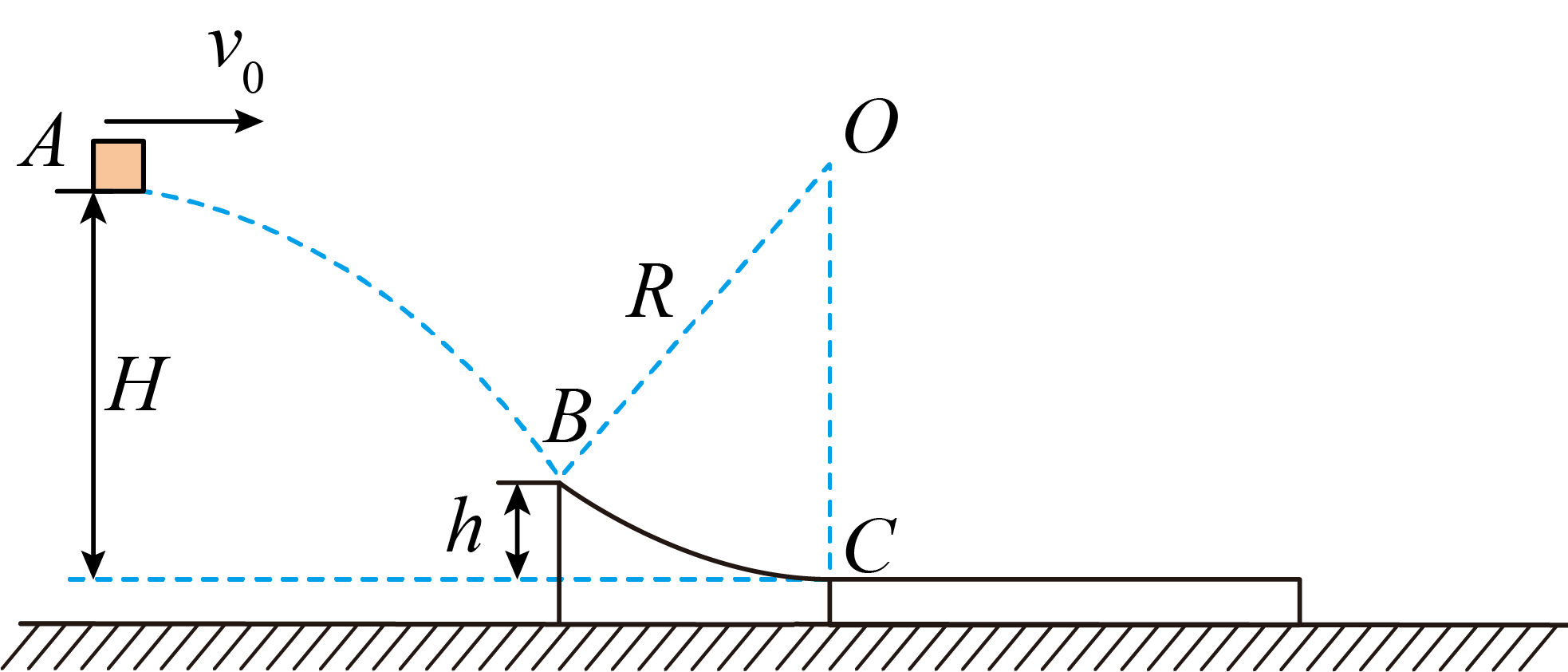
小物块在$A$点抛出时的速度大小；

$v_{0}=4\\;\\rm m/s$

由几何关系可知$h=R(1-\cos 37^\circ )$

解得$h=\dfrac{3}{20}\ \text{m}$

物块从$A$到$B$的过程，竖直方向列运动学关系式$v_{y}^{2}=2g(H-h)$

即可得竖直分速度$v_{y}=3\;\rm m/s$

由几何关系可知，其分速度、合速度关系如下图

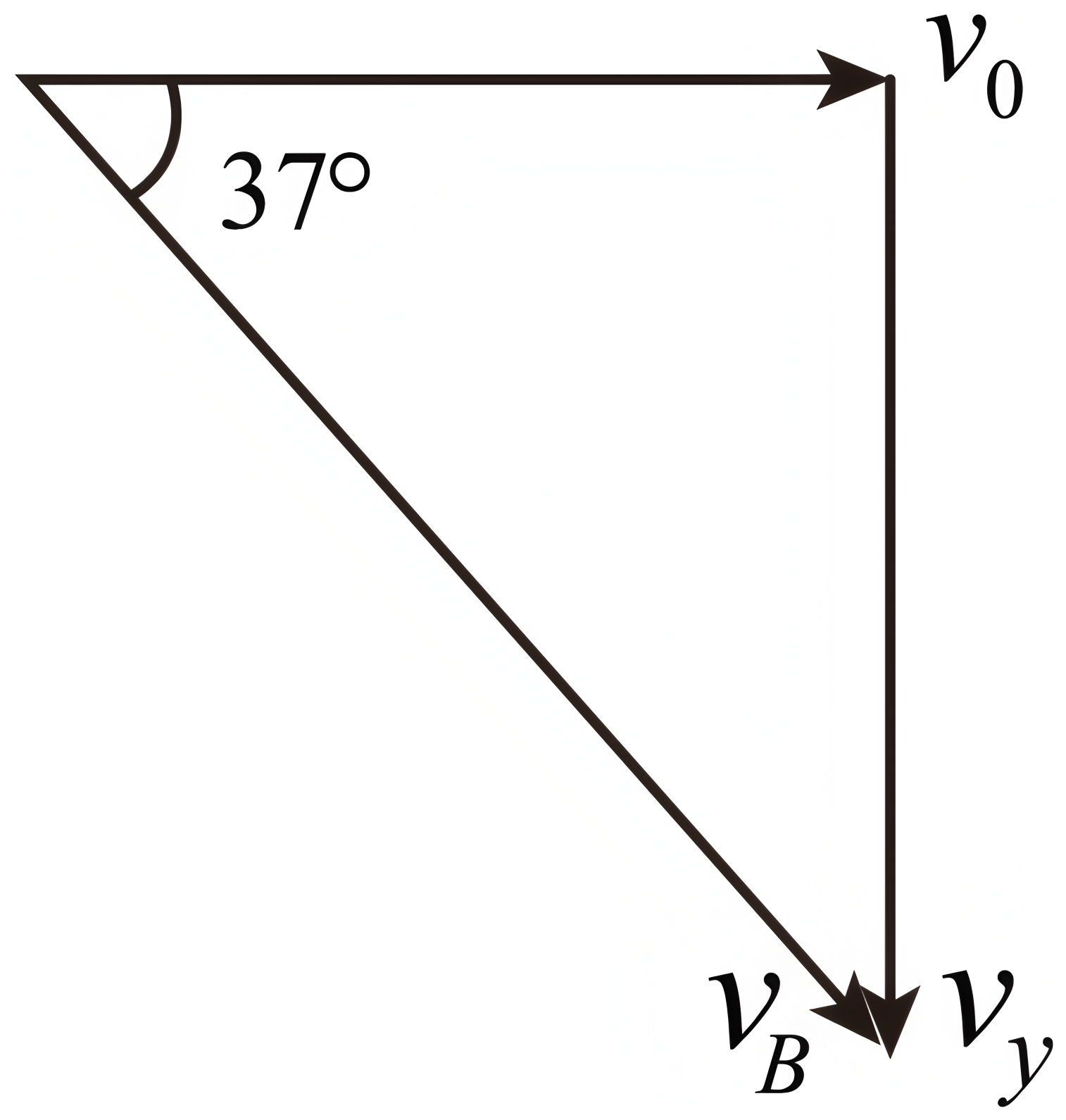
由题意可知物块恰好沿切线进入圆弧轨道，即可知其水平分速度、竖直分速度、合速度满足$\tan 37{{^\circ}}=\dfrac{v_{y}}{v_{0}}$

解得其初速度为$v_{0}=4\;\rm m/s$

小物块滑至圆弧轨道$C$点时的向心加速度大小；

$a_{nc}=12\\;\\rm m/s^{2}$

物块从$B$到$C$的过程，由动能定理$mgh-W=\dfrac{1}{2}mv_{C}^{2}- \dfrac{1}{2}mv_{B}^{2}$

解得其到达$C$点时的速度为$v_{C}=3\;\rm m/s$

由$a_{\text{n}c}=\dfrac{v_{C}^{2}}{R}=12\;\rm \text{m/s}^{\text{2}}$

为保证小物块不滑出长木板，长木板至少为多长？

$L=0.5\\;\\rm m$

以水平向右为正方向，物块和长木板作为整体，在水平方向不受外力，即水平方向动量守恒$mv_{C}=(m+M)v$

解得共同速度为$v=2\;\rm m/s$

由能量守恒$\mu mgL=\dfrac{1}{2}mv_{C}^{2}-\dfrac{1}{2} \times (m+M)v^{2}$

可得长木板的最小长度为$L=0.5\;\rm m$