高中 | 动生电动势 题目答案及解析
稿件来源:高途
高中 | 动生电动势题目答案及解析如下,仅供参考!
选修3-2
第四章 电磁感应
4.5 电磁感应现象的两类情况
动生电动势
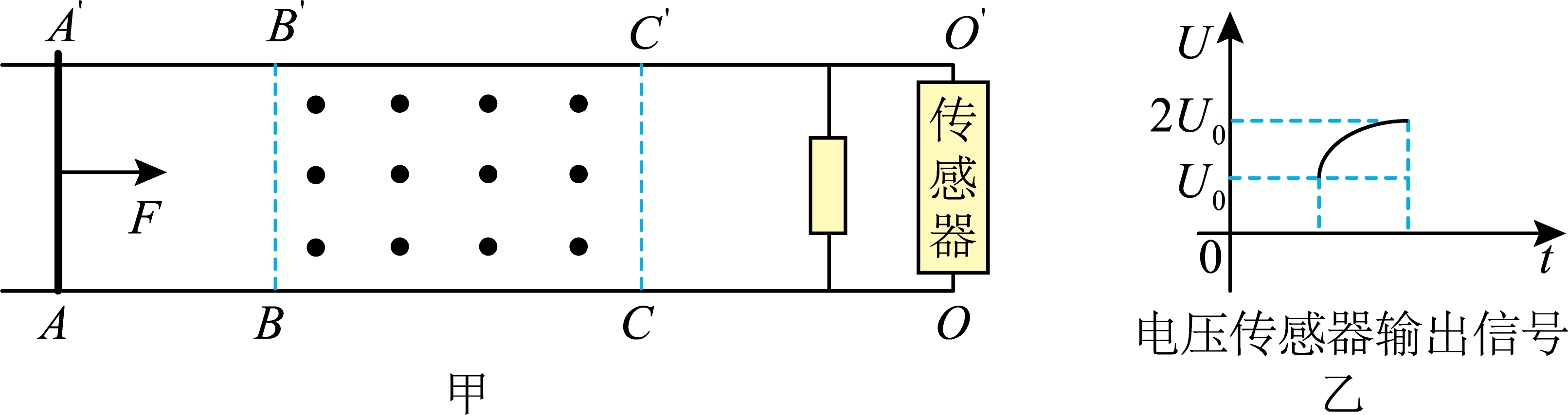
如图甲所示,在水平面上固定两根平行的金属轨道$AO$和$A'O'$,其中$BC$、$B'C'$段长度均为$L$,$BC$、$B'C'$粗糙且动摩擦因数为$\mu $,轨道其余部分光滑。$BB'C'C$区域存在竖直向上的匀强磁场,磁感应强度为$B_{0}$,轨道间连接有阻值为$R$的电阻和一套电压传感器(内阻可视为无穷大)。现有一金属棒,受水平向右的恒力$F$作用,从$AA'$处由静止开始运动,通过数字接收器在屏幕上显示的电压如图乙所示($U_{0}$已知),当电压为$2U_{0}$时曲线已趋向水平。已知金属棒的质量为$m$,电阻也为$R$。轨道间距为$d$,轨道电阻不计。求:
金属棒刚进入磁场时的速度$v_{1}$的大小;
$v_{1}= \\dfrac{2U_{0}}{B_{0}d}$
"]]金属棒刚进入磁场时,产生的感应电动势为$E=B_{0}dv_{1}$
根据闭合电路欧姆定律,有$U_{0}=IR=\dfrac{E}{R+R}R$
解得金属棒刚进入磁场时的速度大小为$v_{1}=\dfrac{2U_{0}}{B_{0}d}$
水平恒力$F$的大小;
$F=\\mu mg+ \\dfrac{2B_{0}U_{0}d}{R}$
"]]根据图像可知$U=2U_{0}$时,电压不再随时间变化,金属棒做匀速运动,金属棒受恒力$F$、安培力和摩擦力三力平衡,所受的安培力为$F_{安}=B_{0}Id= B_{0}\dfrac{2U_{0}}{R}d$
根据平衡条件,有$F=\mu mg+F_{安}$
解得恒力为$F=\mu mg+\dfrac{2B_{0}U_{0}d}{R}$
金属棒经过$BB'C'C$区域的时间$t$;
$t=\\dfrac{mR}{{B_{0}}^{2}d^{2}}+ \\dfrac{B_{0}dL}{4U_{0}}$
"]]金属棒在经过$BC$区域时,受恒力$F$、安培力和摩擦力由动量定理有$Ft-\mu mgt- \dfrac{{B_{0}}^{2}d^{2}\overline{v}}{2R}t=m\left( 2v_{1} \right)- mv_{1}$
解得运动的时间为$t=\dfrac{mR}{{B_{0}}^{2}d^{2}}+\dfrac{B_{0}dL}{4U_{0}}$
金属棒在经过$BB'C'C$区域的过程中,金属棒产生的焦耳热$Q$。
$Q=\\dfrac{B_{0}U_{0}dL}{R}- \\dfrac{3m{U_{0}}^{2}}{{B_{0}}^{2}d^{2}}$
"]]金属棒在经过$BB'C'C$区域的过程中,由动能定理有$(F-\mu mg)L-W_{克安}=\dfrac{1}{2}mv_{2}^{2}- \dfrac{1}{2}mv_{1}^{2}$
且$W_{克安}=2Q$,$v_{2}=2v_{1}$
代入数据解得$2Q=\dfrac{2B_{0}U_{0}dL}{R}-\dfrac{6m{U_{0}}^{2}}{{B_{0}}^{2}d^{2}}$
金属棒产生焦耳热$Q=\dfrac{B_{0}U_{0}dL}{R}-\dfrac{3m{U_{0}}^{2}}{{B_{0}}^{2}d^{2}}$
高中 | 动生电动势题目答案及解析(完整版)
