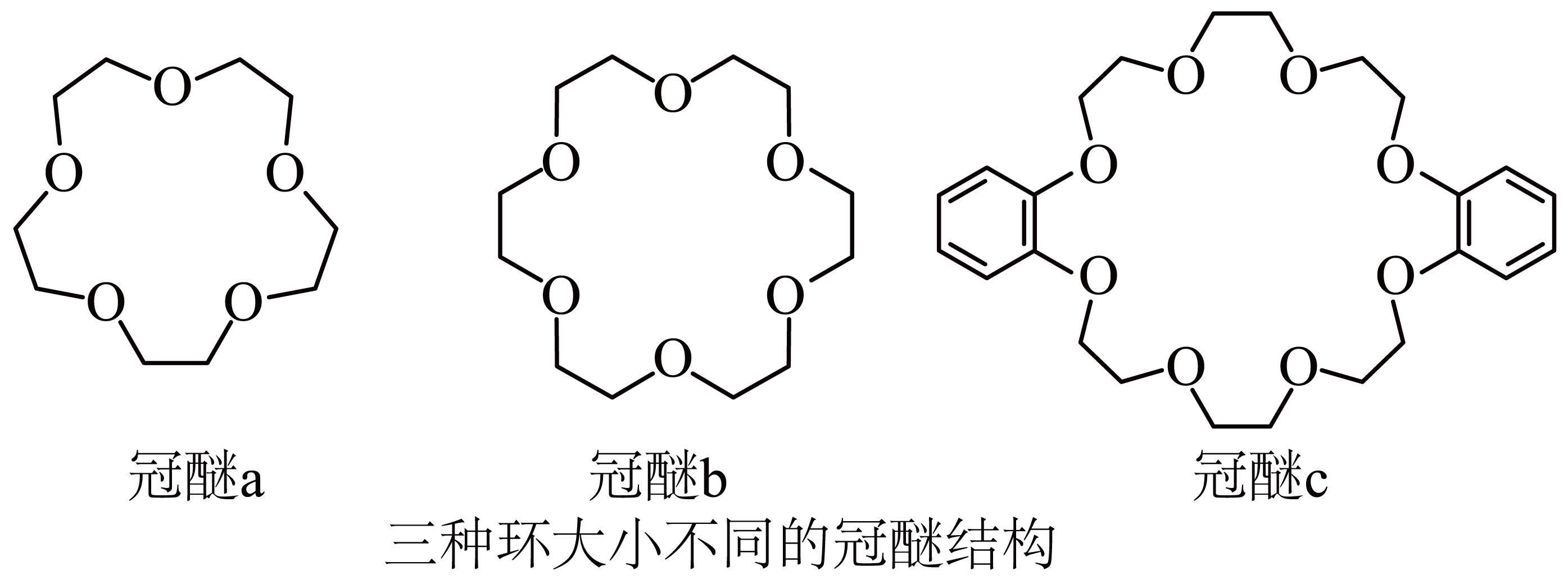
下列冠醚中$\rm O$原子的基态或激发态价电子中，能量由低到高排列的正确顺序为                。

$\\rm ii\\lt i\\lt iii$

能量$\rm 2s\lt 2p\lt 3s\lt 3p$，电子所在能级越高，该微粒能量越高；又由于$\rm i$所示电子排布不符合能量最低原理，所以能量比$\rm ii$高，则能量由低到高的顺序是$\rm ii\lt i\lt iii$。

$\rm KMn{{O}_{4}}$具有强氧化性，$\rm Mn$在元素周期表中的位置是                ，其水溶液对环己烯的氧化效果很差，若将环己烯溶于冠醚$\rm b$再加入$\rm KMn{{O}_{4}}$，氧化效果大幅度提升，原因是                。

第四周期第$\\rm VIIB$族；烯烃与水互不相溶，高锰酸钾与烯烃不易接触，加入冠醚后，烯烃在冠醚中溶解度好，同时$\\rm MnO_{4}^{-}$随钾离子进入冠醚溶液，$\\rm MnO_{4}^{-}$不与冠醚结合，游离的$\\rm MnO_{4}^{-}$与烯烃充分接触，反应活性高，反应速率快

$\rm Mn$元素在周期表中的位置为第四周期第$\rm VIIB$族，根据相似相溶原理知，冠醚可溶于烯烃，加入冠醚中的钾离子因静电作用将高锰酸根离子带入烯烃中，增大反应物的接触面积，提高氧化效果，原因是：烯烃与水互不相溶，高锰酸钾与烯烃不易接触，加入冠醚后，烯烃在冠醚中溶解度好，同时$\rm MnO_{4}^{-}$随钾离子进入冠醚溶液，$\rm MnO_{4}^{-}$不与冠醚结合，游离的$\rm MnO_{4}^{-}$与烯烃充分接触，反应活性高，反应速率快。

分子$\rm A($结构如图所示$\rm )$能与冠醚$\rm c$形成一种分子梭结构，其中$\rm N$的杂化为                ，该分子梭可以通过加入酸或碱使冠醚$\rm c$在位点$\rm 1$和位点$\rm 2$之间来回移动。加酸冠醚$\rm c$移动到位点$\rm 2$，冠醚$\rm c$与位点$\rm 2$之间的相互作用为                。

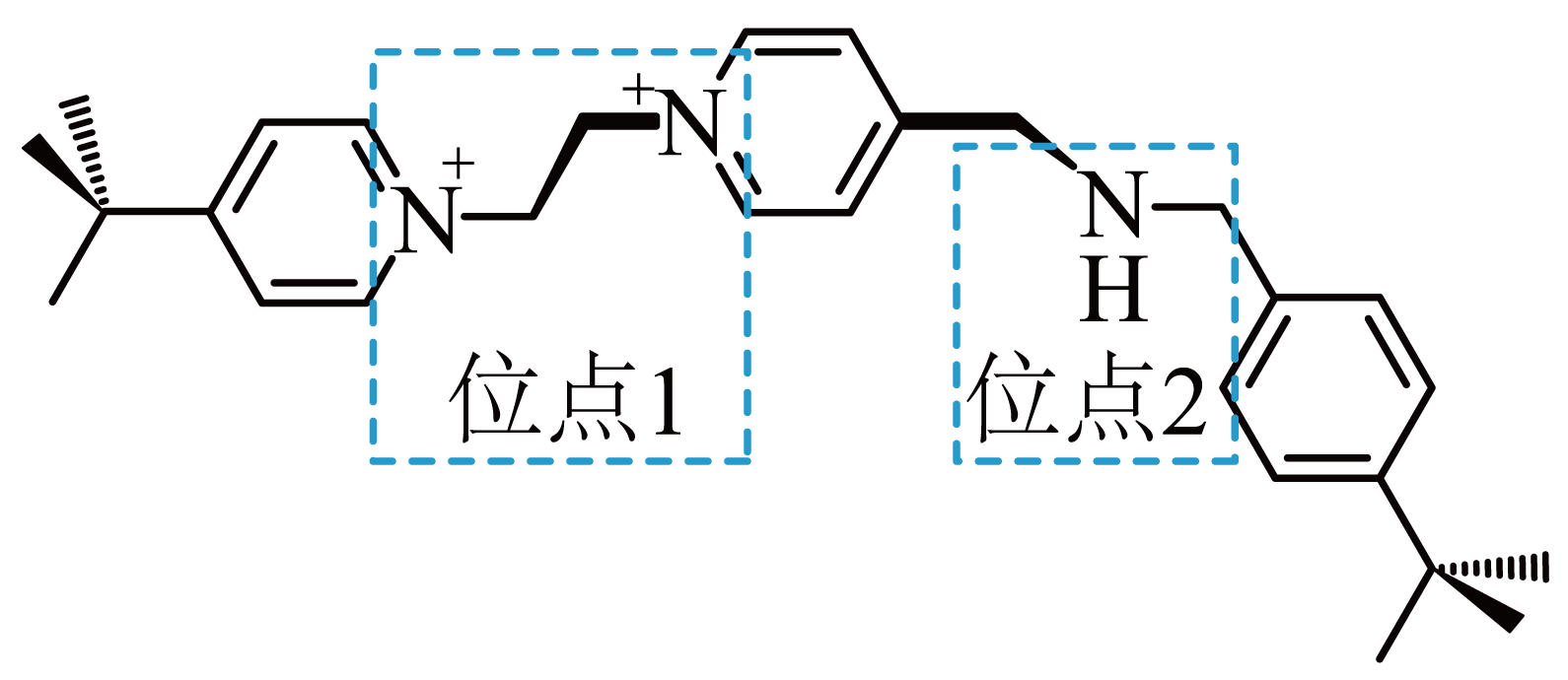
$\rm a$．静电相互作用

$\rm b$．离子键

$\rm c$．共价键

$\rm d$．氢键

$\\rm sp^{2}$、$\\rm sp^{3}$；$\\rm ad$

环上的氮原子的价层电子对数为：$\rm 2+1=3$，故该$\rm N$原子为$\rm sp^{2}$杂化，$\rm -NH-$上的$\rm N$为$\rm sp^{3}$杂化，该分子梭可以通过加入酸或碱使冠醚$\rm c$在位点$\rm 1$和位点$\rm 2$之间来回移动，说明冠醚$\rm c$与位点$\rm 2$之间的相互作用为静电相互作用和氢键，故选：$\rm ad$。

$\rm C{{o}^{2+}}$与冠醚$\rm a$结合能力强，$\rm KCo{{F}_{3}}$有独特的电性、磁性和光致发光性能。

①$\rm C{{o}^{2+}}$的价电子排布式为                。

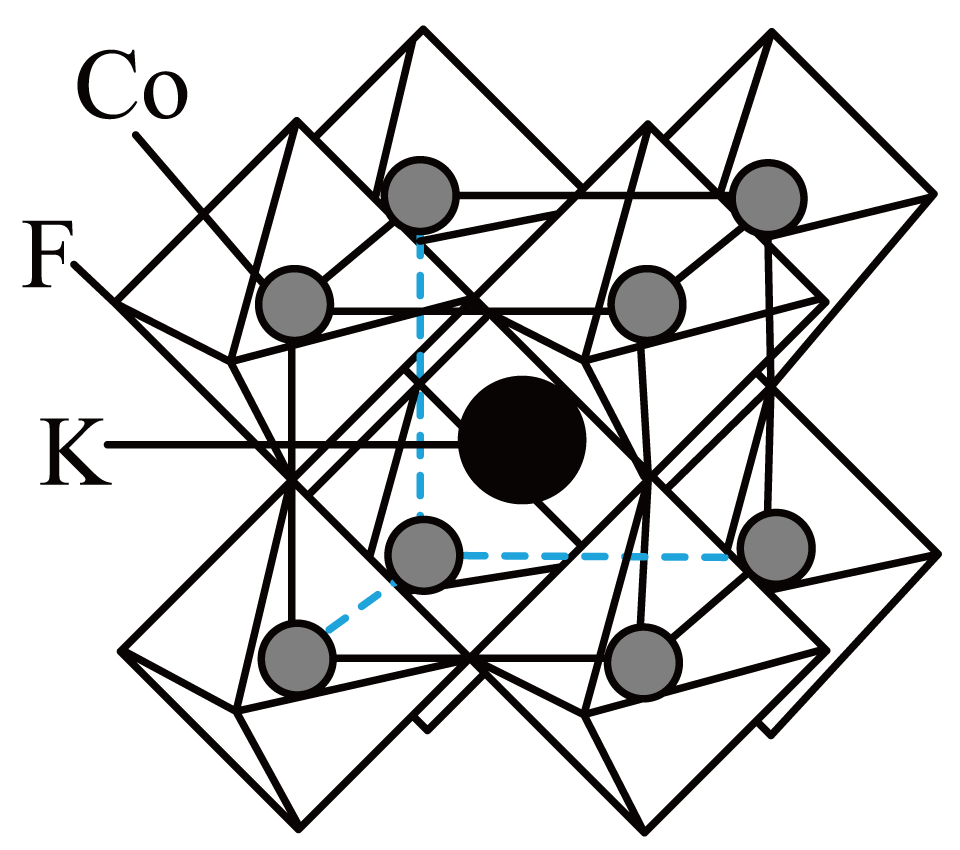
②$\rm KCo{{F}_{3}}$晶体结构如图所示，每个小正八面体的顶点均为$\rm F$原子，该立方晶胞中$\rm Co$的配位数为                ，该晶体密度为$\rm \rho\ g/c{{m}^{3}}$，则该晶胞的棱长为                $\rm pm$。

$\\rm 3d^{7}$；$\\rm 6$；$\\sqrt[3]{\\dfrac{155}{ \\rho{{N}_{\\rm A}}}}\\times {{10}^{10}}$

①$\rm Co$是$\rm 27$号元素，故$\rm Co^{2+}$的价电子排布式为$\rm 3d^{7}$。

②每个小正八面体的顶点均为$\rm F$原子，面心是$\rm Co$原子，该立方晶胞中$\rm Co$的配位数为$\rm 6$；$\rm KCo{{F}_{3}}$晶胞质量$m=\dfrac{155}{{{N}_{\rm A}}}\ \rm g$，设该晶胞的棱长为$a\ \rm pm$，体积为$V=(a\times 10^{-10})^{3}\rm \ cm^{3}$，由晶体密度$\rho =\dfrac{m}{V}$，可得$a=\sqrt[3]{\dfrac{155}{\rho{{N}_{\rm A}}}}\times {{10}^{10}}\ \rm pm$。