已知：反应①  $2\text{N}{{\text{H}}_{3}}\left( \text{g} \right)+3{{\text{N}}_{2}}\text{O}\left( \text{g} \right)\rightleftharpoons 4{{\text{N}}_{2}}\left( \text{g} \right)+3{{\text{H}}_{2}}\text{O}\left( 1 \right)\quad \Delta {{H}_{1}}=-1010\,\text{kJ}\cdot \text{mo}{{\text{l}}^{\text{-1}}}$  

反应②  $4\text{N}{{\text{H}}_{3}}\left( \text{g} \right)+3{{\text{O}}_{2}}\left( \text{g} \right)\rightleftharpoons 2{{\text{N}}_{2}}\left( \text{g} \right)+6{{\text{H}}_{2}}\text{O}\left( 1 \right)\quad \Delta {{H}_{2}}=-1531\,\text{kJ}\cdot \text{mo}{{\text{l}}^{\text{-1}}}$  

已知${{\text{N}}_{2}}\text{O}\left( \text{g} \right)$的热分解反应$2{{\text{N}}_{2}}\text{O}\left( \text{g} \right)\rightleftharpoons 2{{\text{N}}_{2}}\left( \text{g} \right)+{{\text{O}}_{2}}\left( \text{g} \right)$的正反应活化能为${{E}_{\text{a}}}\,\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$，则逆反应活化能为                $\rm ($用含${{E}_{\text{a}}}$的式子表示$\rm )\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$。

$ (E_{\\rm a}+163)$

根据盖斯定律，反应$\dfrac{1}{3}\left( \times 2- \right)$可得$2{{\text{N}}_{2}}\text{O}\left( \text{g} \right)\rightleftharpoons 2{{\text{N}}_{2}}\left( \text{g} \right)+{{\text{O}}_{2}}\left( \text{g} \right)$，$\Delta H=\dfrac{\text{1}}{\text{3}}\left( \text{2}\Delta {{H}_{\text{1}}}-\Delta {{H}_{\text{2}}} \right)=-163\,\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$，正反应活化能为${{E}_{\text{a}}}\,\text{kJ}\cdot \text{mo}{{\text{l}}^{\text{-1}}}$，则逆反应活化能为$ (E_{\rm a}+163)$；

反应$2{{\text{N}}_{2}}\text{O}\left( \text{g} \right)\rightleftharpoons 2{{\text{N}}_{2}}\left( \text{g} \right)+{{\text{O}}_{2}}\left( \text{g} \right)$的经验公式的实验数据如图中曲线$\rm a$所示，已知经验公式为$R\text{lnk}=-{{E}_{\text{a}}}\text{/}T+C ({{E}_{\text{a}}}$为活化能，$T$为热力学温度，$k$为速率常数，$R$和$C$为常数$\rm )$，则该反应的活化能${{E}_{\text{a}}}=$                $\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$；当改变外界条件时，实验数据如图中曲线$\rm b$所示，则实验可能改变的外界条件是                。

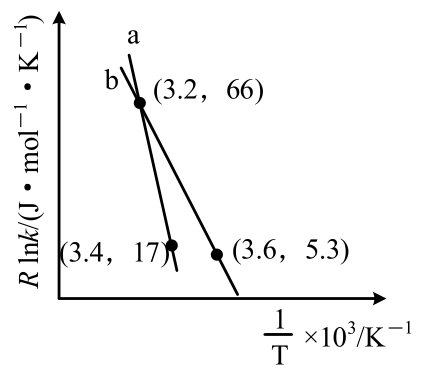
$\\rm 245$ ； 使用更高效的催化剂

根据公式$R\text{lnk}=\dfrac{-{{E}_{\text{a}}}}{T}+C$，将$\rm a$曲线上两点$\rm (3.2$，$\rm 66)$、$\rm (3.4$，$\rm 17)$代入，解得${{E}_{\text{a}}}=\rm 245\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$；

$R\text{lnk}=\dfrac{-{{E}_{\text{a}}}}{T}+C$其中$R$、$C$为常数，不随任何条件下的改变而变化；$k$为速率常数，与温度有关，如图，当改变外界条件时，$\rm a$到$\rm b$的斜率减小，根据公式可知，斜率的相反数为活化能，即斜率较小，活化能降低，则其改变的外界条件可能是加入了更高效的催化剂；

通过加热${{\text{N}}_{2}}{{\text{O}}_{5}}$分解可以得到${{\text{N}}_{2}}\text{O}$：

Ⅰ．${{\text{N}}_{2}}{{\text{O}}_{5}}\left( \text{g} \right)\rightleftharpoons {{\text{N}}_{2}}{{\text{O}}_{3}}\left( \text{g} \right)+{{\text{O}}_{2}}\left( \text{g} \right)$；

Ⅱ．${{\text{N}}_{2}}{{\text{O}}_{3}}\left( \text{g} \right)\rightleftharpoons {{\text{N}}_{2}}\text{O}\left( \text{g} \right)+{{\text{O}}_{2}}\left( \text{g} \right)$。在一定温度下将$2\,\text{mol}\,{{\text{N}}_{2}}{{\text{O}}_{5}}\left( \text{g} \right)$充入$\rm 1$ $\rm L$恒容密闭容器中，反应至$ts$时达到平衡状态，${{\text{O}}_{2}}\left( \text{g} \right)$和${{\text{N}}_{2}}{{\text{O}}_{3}}\left( \text{g} \right)$的物质的量随反应时间的变化关系如图所示。

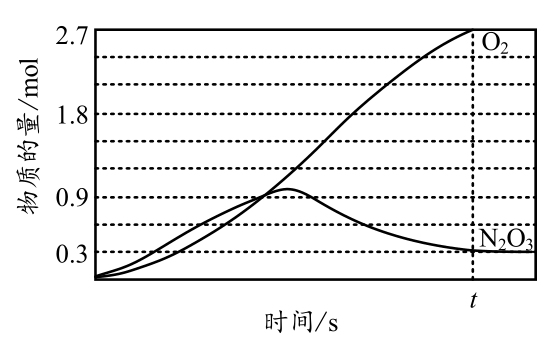
①平衡时${{\text{N}}_{2}}{{\text{O}}_{5}}\left( \text{g} \right)$的转化率为                $\rm \\%$。

②若初始压强为$p$，反应Ⅱ的压强平衡常数${{K}_{\text{p}}}=$                $\rm ($用含$p$的式子表示$\rm )$。

③${{\text{N}}_{2}}{{\text{O}}_{3}}\left( \text{g} \right)$的物质的量随反应时间先增大后减小的原因是                。

$\\rm 75$ ； $\\rm 5.4p$ ； 反应初期，$c\\left( {{\\text{N}}_{\\text{2}}}{{\\text{O}}_{5}} \\right)$较大，反应Ⅰ的反应速率比反应Ⅱ大，随着反应进行$c\\left( {{\\text{N}}_{\\text{2}}}{{\\text{O}}_{5}} \\right)$逐渐减小，$c\\left( {{\\text{N}}_{\\text{2}}}{{\\text{O}}_{\\text{3}}} \\right)$增大，反应Ⅱ的反应速率比反应Ⅰ大，故$\\rm N_{2}O_{3}$物质的量先增大后减小。

①设反应Ⅰ转化$a\,\text{mol}\,{{\text{N}}_{2}}{{\text{O}}_{5}}$，反应Ⅱ转化$b\,\text{mol}\,{{\text{N}}_{2}}{{\text{O}}_{3}}$，列三段式：$\begin{matrix} {} & {{\text{N}}_{2}}{{\text{O}}_{5}}\left( \text{g} \right) & \rightleftharpoons & {{\text{N}}_{2}}{{\text{O}}_{3}}\left( \text{g} \right) & + & {{\text{O}}_{2}}\left( \text{g} \right) \\ 起始\text{(mol)} & 2 & {} & 0 & {} & 0 \\ 转化\text{(mol)} & a & {} & a & {} & a \\ 平衡\text{(mol)} & 2-a & {} & a & {} & a \\ \end{matrix}$，$\begin{matrix} {} & {{\text{N}}_{\text{2}}}{{\text{O}}_{\text{3}}}\left( \text{g} \right) & \rightleftharpoons & {{\text{N}}_{\text{2}}}\text{O}\left( \text{g} \right) & + & {{\text{O}}_{\text{2}}}\left( \text{g} \right) \\ 起始\text{(mol)} & a & {} & \text{0} & {} & a \\转化 \text{(mol)} & b & {} & b & {} & b \\平衡 \text{(mol)} & a-b & {} & b & {} & a+b \\ \end{matrix}$，$a-b=0.3$，$a+b=2.7$，解得$a=1.5\,\text{mol}$，$b=1.2\,\text{mol}$，${{\text{N}}_{2}}{{\text{O}}_{5}}\left( \text{g} \right)$转化率$\dfrac{1.5}{2}\times 100\%=75\%$；

②$n\left( {{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}} \right)=0.5\,\text{mol}$，$n\left( {{\text{N}}_{\text{2}}}{{\text{O}}_{3}} \right)=0.3\,\text{mol}$，$n\left( {{\text{O}}_{\text{2}}} \right)=2.7\,\text{mol}$，$n\left( {{\text{N}}_{\text{2}}}\text{O} \right)=1.2\,\text{mol}$，${{n}_{总}}=4.7\,\text{mol}$，$\dfrac{2\,\text{mol}}{p}=\dfrac{4.7\,\text{mol}}{{{p}_{平}}}\Rightarrow {{p}_{平}}=\dfrac{4.7}{2}p$，${{K}_{\text{p}}}=\dfrac{p\left( {{\text{N}}_{\text{2}}}\text{O} \right)p\left( {{\text{O}}_{\text{2}}} \right)}{p\left( {{\text{N}}_{\text{2}}}{{\text{O}}_{\text{3}}} \right)}=\dfrac{\dfrac{1.2}{4.7}\times \dfrac{4.7}{2}p\dfrac{2.7}{4.7}\times \dfrac{4.7}{2}p}{\dfrac{0.3}{2}p}=5.4p$；

③${{\text{N}}_{2}}{{\text{O}}_{3}}\left( \text{g} \right)$的物质的量随反应时间先增大后减小的原因是：反应初期，$c\left( {{\text{N}}_{\text{2}}}{{\text{O}}_{5}} \right)$较大，反应Ⅰ的反应速率比反应Ⅱ大，随着反应进行$c\left( {{\text{N}}_{\text{2}}}{{\text{O}}_{5}} \right)$逐渐减小，$c\left( {{\text{N}}_{\text{2}}}{{\text{O}}_{\text{3}}} \right)$增大，反应Ⅱ的反应速率比反应Ⅰ大，故$\rm N_{2}O_{3}$物质的量先增大后减小；

$\text{N}{{\text{O}}_{2}}$传感器通常用于大气及环境监测。近日，某课题组利用离子导电水凝胶制备出高性能的传感器，使$\text{N}{{\text{O}}_{2}}$响应发生在电极$\text{CaC}{{\text{l}}_{2}}$水凝胶界面，始终保持良好的响应特性。其工作原理如图所示。

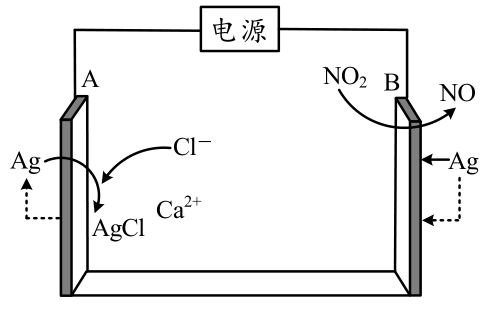
①图中虚线箭头表示的是                $\rm ($填“电子”或“电流”$\rm )$流向。

②$\rm B$电极上发生反应的方程式为                。

电子 ； $\\rm NO_{2}\\rm +\\rm 2e^{−\\rm } \\rm + \\rm H_{2}O \\rm = \\rm NO \\rm + \\rm 2OH^{−\\rm }$

与$\rm B$电极连接的电解池的电极上发生$\rm NO_{2}$变化为$\rm NO$，氮元素化合价降低发生还原反应，判断为阴极，电极反应为$\rm NO_{2}+2e^{−\rm }+H_{2}O=NO+2OH^{−\rm }$，连接电源负极，$\rm A$为阳极，连接电源正极，虚线由$\rm Ag→AgCl$，故虚线表示的为电子流向；