已知${\rm 2H_{2}S(g)+CO_{2}(g)⇌CS_{2}(g)+2H_{2}O(l)}\quad\Delta H=+30\rm \ kJ/mol$，结合下表中甲烷和氢气的燃烧热数值，计算甲烷硫化氢重整制氢反应的$\Delta H=$                。

$\\rm +260\\ kJ/mol$

根据甲烷和氢气的燃烧热数值可得热化学方程式①、②：

① ${\rm C{{H}_{4}}(g)+2{{O}_{2}}(g)=C{{O}_{2}}(g)+2{{H}_{2}}O(l)}\quad\Delta H=-890\rm \ kJ\cdot mo{{l}^{-1}}$；

②  ${\rm 2{{H}_{2}}(g)+{{O}_{2}}(g)=2{{H}_{2}}O(l)}\quad\Delta H=-560\rm \ kJ\cdot mo{{l}^{-1}}$；

已知反应：③  ${\rm 2H_{2}S(g)+CO_{2}(g)\rightleftharpoons CS_{2}(g)+2H_{2}O(l)}\quad\Delta H=+30\rm \ kJ\cdot mo{{l}^{-1}}$；

根据盖斯定律，由① $\rm +$③ $\rm -$② $\rm \times 2$得${\rm CH_{4}(g)+2H_{2}S(g)\rightleftharpoons CS_{2}(g)+4H_{2}(g)}\quad\Delta H=(-890\rm \ kJ\cdot mo{{l}^{-1}})+(+30\ kJ\cdot mo{{l}^{-1}})-(-560\ kJ\cdot mo{{l}^{-1}})\times 2=+260\ kJ\cdot mo{{l}^{-1}}$。

恒压条件下，$\rm CH_{4}$与$\rm H_{2}S$按物质的量比$\rm 1:3$通入反应器，测定$\rm CH_{4}$平衡转化率随温度的变化情况，绘制曲线$\rm M$（见下图）。保持进料口总压、$\rm CH_{4}$与$\rm H_{2}S$物质的量比恒定，通入一定量的$\rm He$作辅气，则曲线应变为                （填“曲线$\rm P$”或“曲线$\rm Q$”），理由是                  。

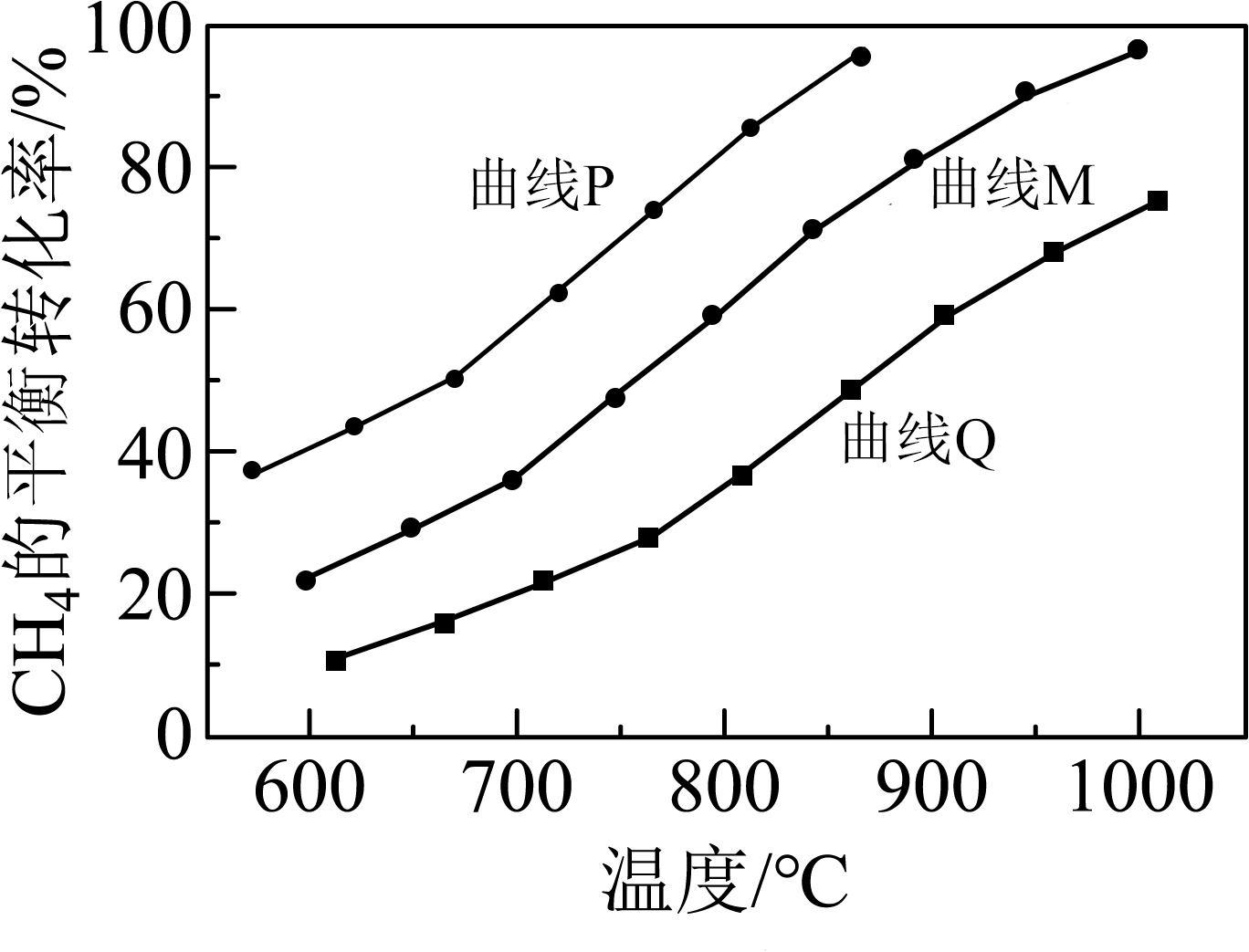
曲线$\\rm P$； 该反应为气体系数和减小的反应，总压一定时，充入$\\rm He$反应物分压减小，平衡向正向移动，相同温度下$\\rm CH_{4}$平衡转化率增大

恒压条件下，$\rm CH_{4}$与$\rm H_{2}S$按物质的量比$\rm 1:3$通入反应器，测定$\rm CH_{4}$平衡转化率随温度的变化情况为曲线$\rm M$所示。保持进料口总压、$\rm CH_{4}$与$\rm H_{2}S$物质的量比恒定，通入一定量的$\rm He$作辅气，由于该反应$\rm CH_{4}(g)+2H_{2}S(g)\rightleftharpoons CS_{2}(g)+4H_{2}(g)$ 为气体系数和增大的反应，总压一定时，充入$\rm He$反应物分压减小，化学平衡正向移动，相同温度下$\rm CH_{4}$平衡转化率增大，则曲线应变为曲线$\rm P$；

假设在恒温$\rm 2\ L$刚性容器中，通入$\rm 4\ mol$ $\rm CH_{4}$、$\rm 4\ mol$ $\rm H_{2}S$和$\rm 2\ mol\ He$作辅气，起始总压为$P_{0}$ $\rm MPa$，$\rm CH_{4}$和$\rm H_{2}S$的转化率与时间的关系如下图。

①用分压的变化表示$\rm 0\sim 5\ min$内$\rm H_{2}$的平均反应速率为                $\rm MPa/min$（分压总压$\rm \times $该气体物质的量分数）。

②可作为该反应达平衡的标志是                （填选项）。

$\rm a$．$\rm CH_{4}$的消耗速率与$\rm CS_{2}$的生成速率之比为$\rm 1:1$            

$\rm b$．$\rm CH_{4}$的体积分数不再变化

$\rm c$．$\dfrac{c{\rm (C{{H}_{4}})}}{c{\rm ({{H}_{2}}S)}}$不再变化                

$\rm d$．混合气体的密度不再改变

③该温度下，反应$\rm CH_{4}(g)+2H_{2}S(g)⇌CS_{2}(g)+4H_{2}(g)$ 的$ K_{x}=$                。$(K_{x}$为物质的量分数平衡常数，用平衡物质的量分数代替平衡浓度计算$\rm )$

$0.032P_{0}$ ；$\\rm bc$ ；$\\rm \\dfrac{4}{27}$或$\\rm 0.15$

①由图可知，$\rm 0\sim 5\ min$内消耗的$\rm H_{2}S$为$\rm 4\ mol\times 20\%=0.8\ mol$。

$\rm \begin{matrix} {} & \rm C{{H}_{4}}(g) & + & \rm 2{{H}_{2}}S(g) & \rightleftharpoons & \rm C{{S}_{2}}(g) & + & \rm 4{{H}_{2}}(g) \\ 初始\rm mol & 4 & {} & 4 & {} & 0 & {} & 0 \\ 变化\rm mol & 0.4 & {} & 0.8 & {} & 0.4 & {} & 1.6 \\ \rm 5\ min \ mol & 3.6 & {} & 3.2 & {} & 0.4 & {} & 1.6 \\ \end{matrix}$

则$\rm 5\ min$时气体的总物质的量为：$\rm 3.6\ mol+3.2\ mol+0.4\ mol+1.6\ mol+2\ mol=10.8\ mol$，反应后的总压为$\dfrac{10.8}{10}{{P}_{0}}$。用分压的变化表示$\rm 0\sim 5\ min$内$\rm H_{2}$的平均反应速率 $=\dfrac{\dfrac{1.6}{10.8}\times \dfrac{10.8}{10}{{P}_{0}}}{5}\ {\rm MPa/min}=0.032P_{0}$ $\rm MPa/min$；

②$\rm a$．$\rm CH_{4}$的消耗速率与$\rm CS_{2}$的生成速率方向相同，$\rm CH_{4}$的消耗速率与$\rm CS_{2}$的生成速率之比为$\rm 1:1$不能说明正逆反应速率相等，不能证明反应达到化学平衡状态，$\rm a$不符合题意；           

$\rm b$．$\rm CH_{4}$的体积分数不再变化，说明$\rm CH_{4}$的生成速率与消耗速率相等，正逆反应速率相等，能证明反应达到化学平衡状态，$\rm b$符合题意；

$\rm c$．刚开始加入的$c{\rm (C{{H}_{4}})}$和$c{\rm ({{H}_{2}}S)}$相等，但甲烷和硫化氢在反应中消耗的速率不同，如果$\dfrac{c{\rm (C{{H}_{4}})}}{c{\rm ({{H}_{2}}S)}}$不再变化，说明二者浓度不再发生变化，证明反应达到化学平衡状态，$\rm c$符合题意；                

$\rm d$．该反应中反应物和生成物均为气体，无论反应是否达到化学平衡状态，混合气体的密度均不会改变，$\rm d$不符合题意；

③由图可知，达到化学平衡状态时$\rm H_{2}S$转化率为$\rm 50\%$，消耗$\rm H_{2}S$为$\rm 4\ mol\times 50\%=2\ mol$。

$\rm \begin{matrix} {} &\rm C{{H}_{4}}(g) & + & \rm 2{{H}_{2}}S(g) & \rightleftharpoons & \rm C{{S}_{2}}(g) & + & \rm 4{{H}_{2}}(g) \\ 初始\rm mol & 4 & {} & 4 & {} & 0 & {} & 0 \\ 变化\rm mol & 1 & {} & 2 & {} & 1 & {} & 4 \\ 平衡\rm mol & 3 & {} & 2 & {} & 1 & {} & 4 \\ \end{matrix}$

则平衡时气体的总物质的量为：$\rm 3\ mol+2\ mol+1\ mol+4\ mol+2\ mol=12\ mol$，该温度下，反应$\rm CH_{4}(g)+2H_{2}S(g)\rightleftharpoons CS_{2}(g)+4H_{2}(g)$ 的$K_{x}=\dfrac{(\dfrac{4}{12}{{)}^{4}}\times \dfrac{1}{12}}{(\dfrac{2}{12}{{)}^{2}}\times \dfrac{3}{12}}=\dfrac{4}{27}≈0.15$。

阿伦尼乌斯公式表示了速率常数与温度、活化能的关系，公式为$k=A{{\rm e}^{-\dfrac{{{E}_{\rm a}}}{RT}}}$，其中$k$为速率常数，$A$和$R$为常数，$R≈8.3\rm \ J/(mol\cdot K)$，$\rm e$为自然对数的底，$E_{\rm a}$为反应的活化能，$T$为开氏温度。已知在温度为$\rm 300\ K$时，甲烷硫化氢重整制氢使用$\rm Mo/Al_{2}O_{3}$催化剂活化能比原来降低$\rm 24.9\ kJ/mol$，则速率常数变为原来的                倍。

$\\rm {{e}^{10}}$

根据阿伦尼乌斯公式为$k=A{{\rm e}^{-\dfrac{{{E}_{\rm a}}}{RT}}}$，其中$k$为速率常数，$A$和$R$为常数，$R≈8.3\rm \ J/(mol\cdot K)$，$\rm e$为自然对数的底，$E_{\rm a}$为反应的活化能，$T$为开氏温度。已知在温度为$300\ \rm K$时，甲烷硫化氢重整制氢使用$\rm Mo/Al_{2}O_{3}$催化剂活化能比原来降低$\rm 24.9\ kJ/mol$，设原速率常数为$k_{1}$，使用$\rm Mo/Al_{2}O_{3}$催化剂时的速率常数为$k_{2}$，$\dfrac{{{k}_{2}}}{{{k}_{1}}}=\dfrac{A{{\rm e}^{-\dfrac{{{E}_{\rm a}}-\Delta {{E}_{\rm a}}}{RT}}}}{A{{\rm e}^{-\dfrac{{{E}_{\rm a}}}{RT}}}}={{\rm e}^{\dfrac{\Delta {{E}_{\rm a}}}{RT}}}$，代入数据可得：$\dfrac{{{k}_{2}}}{{{k}_{1}}}={{\rm e}^{\dfrac{\Delta {{E}_{\rm a}}}{RT}}}={{\rm e}^{\dfrac{24.9\times {{103}}}{8.3\times 300}}}={{\rm e}^{10}}$。

已知$\rm Mo/Al_{2}O_{3}$催化剂表面的活性位点数量是决定该催化剂活性的重要因素，当原料中甲烷含量较高时会裂解产生积炭，导致催化剂活性降低，分析可能的原因是                  。

积碳覆盖了催化剂的活性位点

当原料中甲烷含量较高时会裂解产生积炭，积碳覆盖了催化剂的活性位点，使催化剂的催化效率减小，从而导致催化剂活性降低。