根据下表数据计算$\Delta {{H}_{\text{1}}}=$                。

$\\rm +34$ $\\rm kJ\\cdot mol^{-1}$

焓变$\rm =$反应物总键能$\rm -$生成物总键能，$\Delta {{H}_{1}}=\left( 463+413\times 9+351\times 3+348\times 3+745 \right)\,\text{kJ}\cdot \text{mo}{{\text{l}}^{\text{-1}}}-\left( 413\times 8+615+745+351\times 2+348\times 2+463\times 2 \right)\,\text{kJ}\cdot \text{mo}{{\text{l}}^{\text{-1}}}=+34\,\text{kJ}\cdot \text{mo}{{\text{l}}^{\text{-1}}}$；

$\rm I$$\rm I$．工业上还可用“丙烯氨氧化法”制备丙烯腈，以丙烯、氨气和氧气为原料，在催化剂作用下制备丙烯腈的主要反应如下：

反应$ 1\ {{\text{C}}_{3}}{{\text{H}}_{6}}\left( \text{g} \right)+\text{N}{{\text{H}}_{3}}\left( \text{g} \right)+\dfrac{3}{2}{{\text{O}}_{2}}\left( \text{g} \right)\rightleftharpoons \text{C}{{\text{H}}_{2}}=\text{CHCN}\left( \text{g} \right)+3{{\text{H}}_{2}}\text{O}\left( \text{g} \right)\quad \Delta {{H}_{1}}=-515\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$  

反应$ 2\ {{\text{C}}_{3}}{{\text{H}}_{6}}\left( \text{g} \right)+{{\text{O}}_{2}}\left( \text{g} \right)\rightleftharpoons \text{C}{{\text{H}}_{2}}=\text{CHCHO}\left( \text{g} \right)+{{\text{H}}_{2}}\text{O}\left( \text{g} \right)\quad \Delta {{H}_{2}}=-353\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$  

首先需合成原料氨气，在反应${{\text{N}}_{2}}\left( \text{g} \right)+3{{\text{H}}_{2}}\left( \text{g} \right)\rightleftharpoons 2\text{N}{{\text{H}}_{3}}\left( \text{g} \right)\quad \Delta H\lt 0$  中，${{v}_{正}}={{k}_{正}}c\left( {{\text{N}}_{2}} \right)\cdot {{c}^{3}}\left( {{\text{H}}_{2}} \right)$，${{v}_{逆}}={{k}_{逆}}{{c}^{2}}\left( \text{N}{{\text{H}}_{3}} \right)$，${{k}_{正}}$、${{k}_{逆}}$为速率常数。正反应和逆反应的平衡常数与温度的关系如图$\rm 1$所示。表示逆反应的平衡常数与温度变化关系的曲线为                $\rm ($填“${{\text{L}}_{\text{1}}}$”或“${{\text{L}}_{\text{2}}}$”$\rm )$，${{T}_{0}}\rm ^\circ\rm C$时，$\dfrac{{{k}_{正}}}{{{k}_{逆}}}=$                。

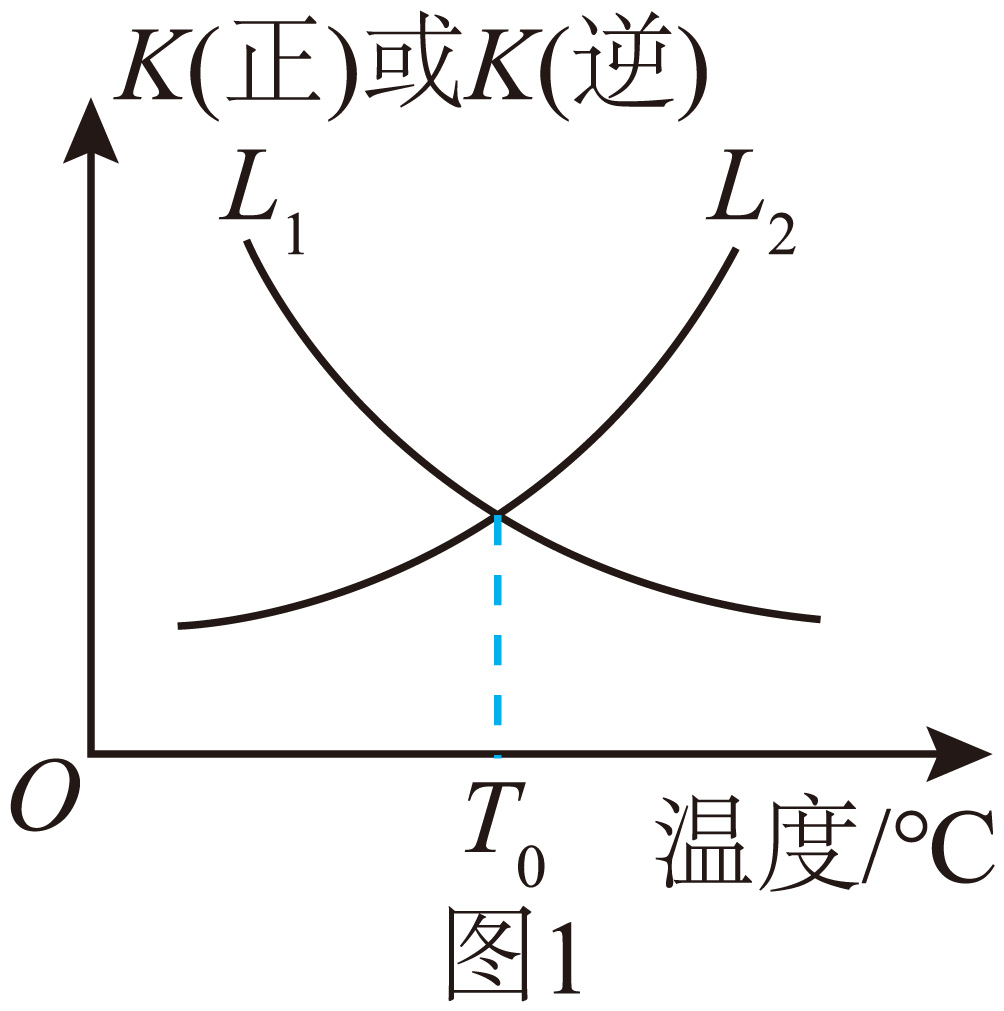
$\\rm L_{2}$ ； $\\rm 1$

该反应为放热反应，升高温度平衡逆向移动，逆反应平衡常数增大，则$\rm L_{2}$表示逆反应的平衡常数与温度变化关系，${{T}_{0}}\text{ }{}^\circ \text{C}$时，正逆平衡常数相等，即$K(正)=K(逆)=1$，平衡时：${{v}_{正}}={{v}_{逆}}$，即${{k}_{正}}\cdot c\left( {{\text{N}}_{\text{2}}} \right)\cdot {{c}^{3}}\left( {{\text{H}}_{\text{2}}} \right)={{k}_{逆}}\cdot {{c}^{2}}\left( \text{N}{{\text{H}}_{\text{3}}} \right)$， $\dfrac{{{k}_{正}}}{{{k}_{逆}}}=\dfrac{{{c}^{\text{2}}}\left( \text{N}{{\text{H}}_{\text{3}}} \right)}{c({{\text{N}}_{\text{2}}})\cdot {{c}^{\text{3}}}({{\text{H}}_{\text{2}}})}={{K}_{正}}=1$；

反应$\rm 1$在                $\rm ($填“高温”“低温”或“任意温度”$\rm )$下可自发进行；恒温恒容条件下，若容器内只发生反应$\rm 1$，下列能表明反应已经达到平衡状态的是                $\rm ($填字母$\rm )$。

$\rm A$．容器内混合气体的密度不再变化

$\rm B$．断裂$1\ \text{mol}\,\text{N}-\text{H}$的同时断裂$\text{3}\,\text{mol}\,\text{O-H}$

$\rm C$．容器内压强不再变化

$\rm D$．$3{{v}_{正}}\left( \text{N}{{\text{H}}_{3}} \right)=2{{v}_{逆}}\left( {{\text{O}}_{2}} \right)$

任意温度 ； $\\rm CD$

反应$\rm 1$的$\Delta H\lt 0$，$\Delta S\gt 0$，$\Delta G=\Delta H-T\Delta S$始终小于$\rm 0$，则在任意温度下都能自发进行；

$\rm A$．容器恒容，密度始终不变，容器内混合气体的密度不再变化不能说明达到平衡，故$\rm A$不选；

$\rm B$．断裂$1\ \text{mol}\,\text{N}-\text{H}$的同时断裂$\text{3}\,\text{mol}\,\text{O-H}$，正逆反应速率不等，没有达到平衡，应该是断裂$1\ \text{mol}\,\text{N}-\text{H}$的同时断裂$\text{2}\,\text{mol}\,\text{O-H}$，反应才平衡，故$\rm B$不选；

$\rm C$．该反应是气体分子数变大的反应，如果没有平衡，向右进行时则压强增大，现压强不变可以说明达到平衡，故$\rm C$选；

$\rm D$．$3{{v}_{正}}\left( \text{N}{{\text{H}}_{3}} \right)=2{{v}_{逆}}\left( {{\text{O}}_{2}} \right)$，速率之比等于计量数之比，反应达到平衡，故$\rm D$选；

在温度为${{T}_{1}}\text{ }{}^\circ \text{C}$和压强为$28\,\text{MPa}$条件下，向恒压密闭容器中充入$1\ \text{mol}\,\text{C}{{\text{H}}_{2}}=\text{CHC}{{\text{H}}_{3}}$、$1\ \text{mol}\,\text{N}{{\text{H}}_{3}}$和$4.8\ \text{mol}\,{{\text{O}}_{2}}$发生上述两个反应，容器内${{\text{H}}_{2}}\text{O}\left( \text{g} \right)$、$\text{C}{{\text{H}}_{2}}=\text{CHCN}\left( \text{g} \right)$、$\text{C}{{\text{H}}_{2}}=\text{CHC}{{\text{H}}_{3}}\left( \text{g} \right)$的物质的量$ (n\rm )$随时间$ (t\rm )$的变化关系如图$\rm 2$所示。图中表示$\text{C}{{\text{H}}_{2}}=\text{CHCN}\left( \text{g} \right)$的曲线是                $\rm ($填“$\rm I$”“$\rm II$”或“$\rm III$”$\rm )$。反应$\rm 2$的压强平衡常数${{K}_{\text{p}}}=$                $({{K}_{\text{p}}}$为用分压表示的平衡常数，分压$\rm =$总压$\rm \times $物质的量分数$\rm )$。

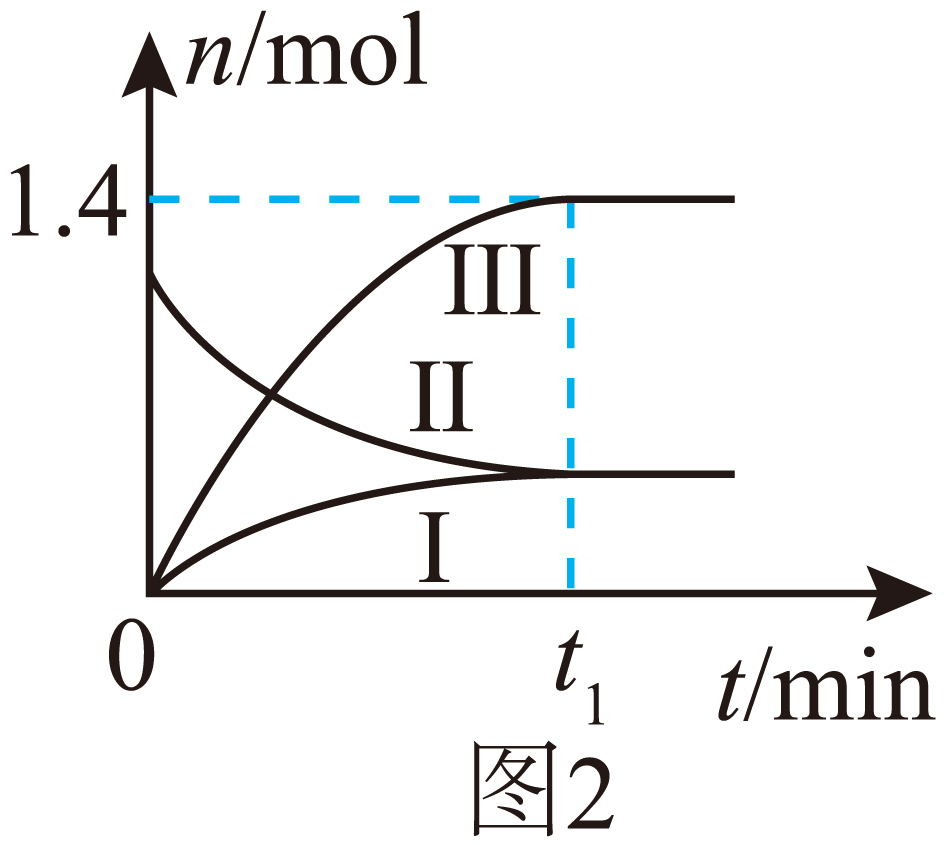
$\\rm I$ ； $\\dfrac{7}{40}$

根据两个反应方程式：

反应$\rm 1{{\text{C}}_{3}}{{\text{H}}_{6}}\left( \text{g} \right)+\text{N}{{\text{H}}_{3}}\left( \text{g} \right)+\dfrac{3}{2}{{\text{O}}_{2}}\left( \text{g} \right)\rightleftharpoons \text{C}{{\text{H}}_{2}}=\text{CHCN}\left( \text{g} \right)+3{{\text{H}}_{2}}\text{O}\left( \text{g} \right)$  

反应$\rm 2{{\text{C}}_{3}}{{\text{H}}_{6}}\left( \text{g} \right)+{{\text{O}}_{2}}\left( \text{g} \right)\rightleftharpoons \text{C}{{\text{H}}_{2}}=\text{CHCHO}\left( \text{g} \right)+{{\text{H}}_{2}}\text{O}\left( \text{g} \right)$

两个反应均正向进行，$\rm H_{2}O$增加的量最大，即曲线$\rm III$表示$\rm H_{2}O$，曲线$\rm II$表示$\rm C_{3}H_{6}$，曲线$\rm I$表示$\text{C}{{\text{H}}_{2}}=\text{CHCN}\left( \text{g} \right)$，假设反应$\rm 1$消耗$\rm C_{3}H_{6}$为$x\,\text{mol}$，反应$\rm 2$消耗$\rm C_{3}H_{6}$为$y\,\text{mol}$，则有：

$\begin{matrix} {} & \text{N}{{\text{H}}_{\text{3}}}\left( \text{g} \right)+ & {{\text{C}}_{\text{3}}}{{\text{H}}_{\text{6}}}\left( \text{g} \right)+ & \dfrac{\text{3}}{\text{2}}{{\text{O}}_{\text{2}}}\left( \text{g} \right) & \rightleftharpoons & \text{C}{{\text{H}}_{\text{2}}}\text{=CHCN}\left( \text{g} \right) & \text{+3}{{\text{H}}_{\text{2}}}\text{O}\left( \text{g} \right) \\变化 \text{(mol)} & {x} & x & \dfrac{3}{2}x & {} & x & 3x \\ \end{matrix}$

$\begin{matrix} {} & {{\text{C}}_{\text{3}}}{{\text{H}}_{\text{6}}}\left( \text{g} \right)+ & {{\text{O}}_{\text{2}}}\left( \text{g} \right) & \rightleftharpoons & \text{C}{{\text{H}}_{\text{2}}}\text{=CHCHO}\left( \text{g} \right) & +{{\text{H}}_{\text{2}}}\text{O}\left( \text{g} \right) \\变化 \text{(mol)} & y & y & {} & y & y \\ \end{matrix}$

根据题意有$3x+y=1.4$，$1-x-y=x$，解得$x=0.4$，$y=0.2$，平衡时$n\left( {{\text{C}}_{\text{3}}}{{\text{H}}_{\text{6}}} \right)=0.4\,\text{mol}$，$n\left( \text{N}{{\text{H}}_{\text{3}}} \right)=1-0.4=0.6\,\text{mol}$，$n\left( {{\text{O}}_{\text{2}}} \right)=4.8-0.6-0.2=4\,\text{mol}$， $n(\text{C}{{\text{H}}_{2}}=\text{CHCN})=0.4\,\text{mol}$，$n\left( {{\text{H}}_{\text{2}}}\text{O} \right)=1.4\,\text{mol}$， $n(\text{C}{{\text{H}}_{2}}=\text{CHCHO})=0.2\,\text{mol}$，$n总=7.0\,\text{mol}$，反应$\rm 2$的压强平衡常数${{K}_{p}}=\dfrac{p({{\text{H}}_{\text{2}}}\text{O})p(\text{C}{{\text{H}}_{2}}=\text{CHCHO})}{p({{\text{C}}_{\text{3}}}{{\text{H}}_{6}})p\text{(}{{\text{O}}_{\text{2}}}\text{)}}=\dfrac{28\times \dfrac{1.4}{7}\times 28\times \dfrac{0.2}{7}}{28\times \dfrac{0.4}{7}\times 28\times \dfrac{4}{7}}=\dfrac{7}{40}$；

$\rm II$$\rm I$．利用电解法由丙烯腈制备己二腈$\left[ \text{NC}{{\left( \text{C}{{\text{H}}_{2}} \right)}_{4}}\text{CN} \right]$的装置示意图如图$\rm 3$所示。

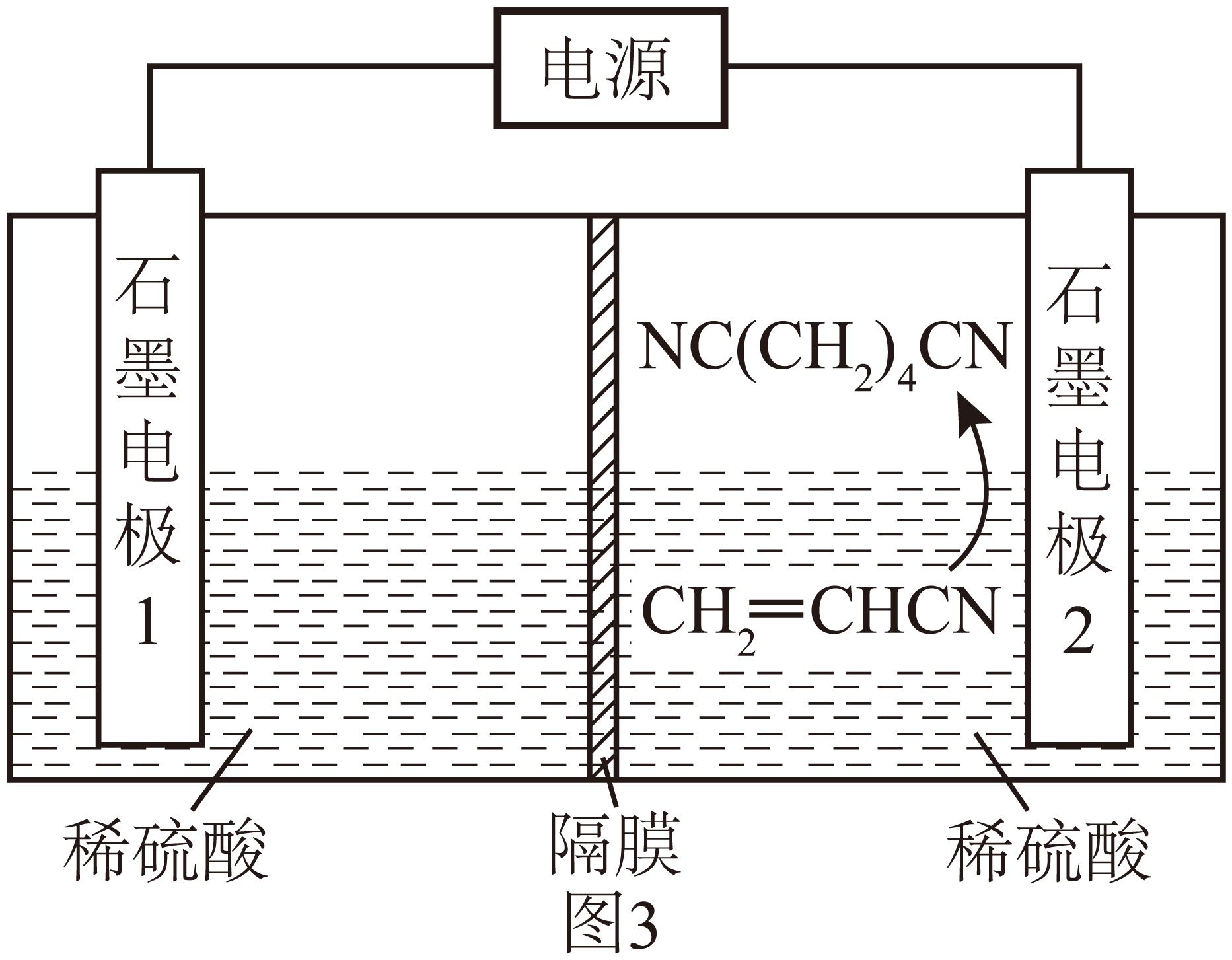
通电过程中，石墨电极$\rm 2$上的电极反应为                。

$\\rm 2CH_{2}=CHCN+2e^{-}+2H^{+}=NC(CH_{2})_{4}CN$

根据图示，石墨电极$\rm 2$上$\rm CH_{2}=CHCN$ 发生还原反应生成$\rm NC(CH_{2})_{4}CN$，石墨电极$\rm 2$上极反应式为$\rm 2CH_{2}=CHCN+2e^{-}+2H^{+}=NC(CH_{2})_{4}CN$

$\text{C}{{\text{H}}_{2}}=\text{CHCN}$转化为$\text{NC}{{\left( \text{C}{{\text{H}}_{2}} \right)}_{4}}\text{CN}$过程中，$\rm C$原子的杂化轨道类型是否发生变化？                $\rm ($填“是”或“否”$\rm )$。

是

$\text{C}{{\text{H}}_{2}}=\text{CHCN}$中$\rm C$原子的杂化类型为$\rm sp$和$\rm sp^{2}$，$\text{NC}{{\left( \text{C}{{\text{H}}_{2}} \right)}_{4}}\text{CN}$中$\rm C$原子的杂化类型为$\rm sp$和$\rm sp^{3}$，杂化方式发生了变化。