金刚石与${{\text{C}}_{60}}$的晶胞结构如图，比较二者熔点大小：金刚石                ${{\text{C}}_{60}}\rm ($填“$\gt $”、“$\lt $”或“$=$”$\rm )$，并从结构角度分析原因                。

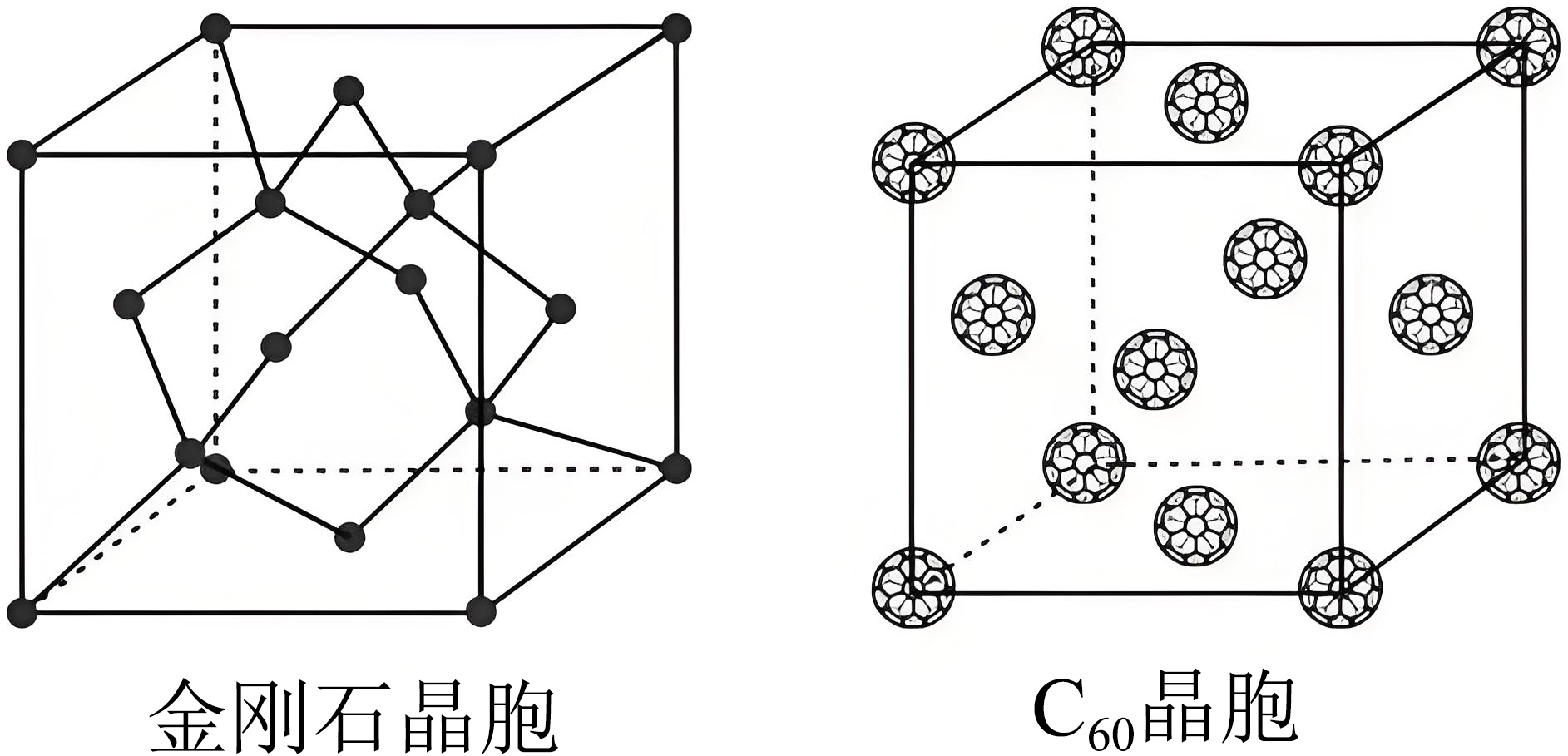
$\\gt $；金刚石是共价晶体，${{\\text{C}}_{60}}$晶体是分子晶体，二者熔化时分别破坏共价键和分子间作用力，共价键的强度大于分子间作用力，故金刚石熔点高于${{\\text{C}}_{60}}$

金刚石的熔点大于${{\text{C}}_{60}}$，因为金刚石为共价晶体， ${{\text{C}}_{60}}$为分子晶体，二者熔化时分别破坏共价键和分子间作用力，共价键的强度大于分子间作用力，故金刚石熔点高于${{\text{C}}_{60}}$。

一种金属富勒烯配合物合成过程如图所示。已知：烯烃、${{\text{C}}_{60}}$等因能提供$\text{ }\!\!\pi$电子与中心原子形成配位键，被称为“$\text{ }\!\!\pi$配体”。

①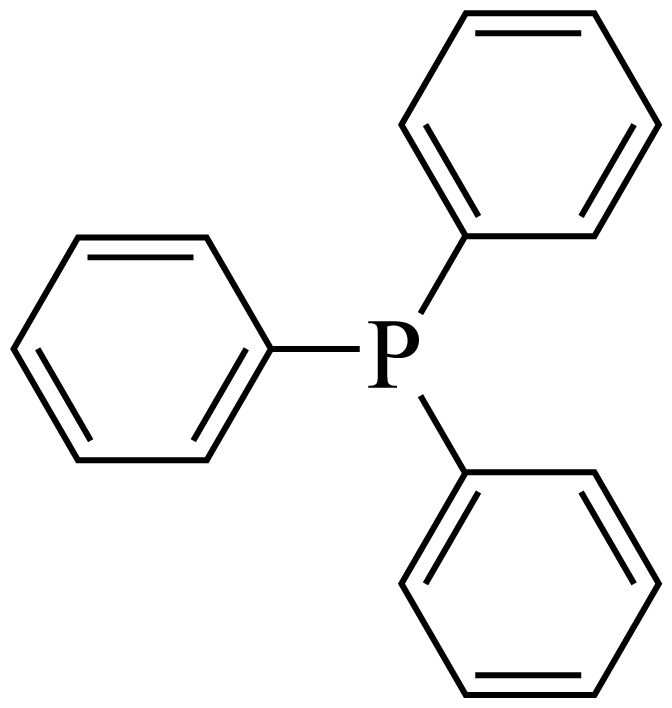$\rm (\text{PP}{{\text{h}}_{3}}\rm )$内中心$\rm P$原子的杂化轨道类型是                。

②比较两种$\pi$配体与$\rm Pt$的配位能力大小：${{\text{C}}_{2}}{{\text{H}}_{4}}$                ${{\text{C}}_{60}}\rm ($填“$\gt $”、“$\lt $”或“$=$”$\rm )$。

③结合${{\text{C}}_{60}}$中$\rm C$原子的成键特点，分析${{\text{C}}_{60}}$可作为$\pi$配体的原因                。

$\\text{s}{{\\text{p}}^{3}}$；$<$；$\\text{C}_{60}$中每个$\\rm C$原子形成$\\rm 3$个$\\sigma\\!\\!\\text{ }$键，未参与形成$\\sigma$键的电子形成大$\\text{ }\\!\\!\\pi$键，故能提供$\\pi\\!\\!\\text{ }$电子与中心原子形成配位键

① 三苯基膦中，中心$\rm P$原子形成$\rm 3$个$\sigma\!\!\text{ }$键和$\rm 1$个孤电子对，为$\text{s}{{\text{p}}^{\text{3}}}$杂化；

②${{\text{C}}_{2}}{{\text{H}}_{4}}{{\text{C}}_{60}}$都是$\pi$配体，能够通过$\pi$电子与中心金属原子形成配位键，${{\text{C}}_{60}}$分子由$\rm 60$个碳原子组成，形成球状结构，每个碳原子通过$\text{s}{{\text{p}}^{\text{2}}}$杂化与相邻的三个碳原子形成$\sigma$键，未参与杂化的一个$\text{p}$轨道上的电子形成离域$\pi$键，具有更大的$\pi$电子云，因此其配位能力更强，则与$\rm Pt$的配位能力大小：${{\text{C}}_{2}}{{\text{H}}_{4}}\lt {{\text{C}}_{60}}$。

③${{\text{C}}_{60}}$分子由$\rm 60$个碳原子组成，形成球状结构，每个碳原子通过$\rm sp^{2}$杂化与相邻的三个碳原子形成$\sigma$键，未参与杂化的一个$\text{p}$轨道上的电子形成离域$\pi$键，这种离域$\pi$键能够提供$\pi$电子与中心原子形成配位键。

${{\text{C}}_{60}}$的碱金属$\rm (\text{M}=\text{K}$、$\rm Rb$、$\rm Cs)$衍生物的晶胞结构如图。

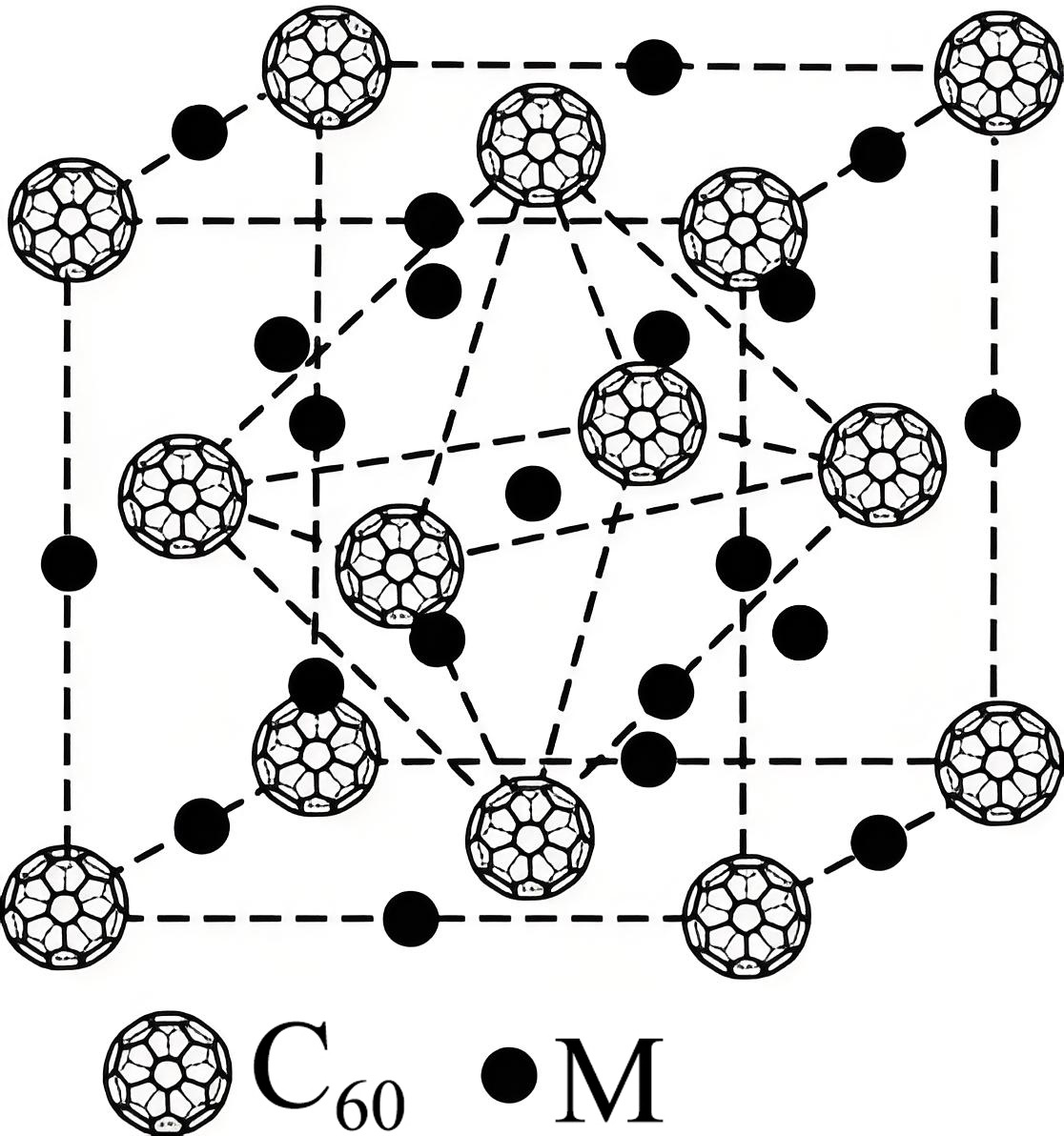
①与每个${{\text{C}}_{60}}$分子紧邻且等距的${{\text{C}}_{60}}$分子数目为                。

②某种${{\text{C}}_{60}}$的碱金属衍生物的化学式为${{\text{M}}_{3}}{{\text{C}}_{60}}$，每个晶胞中含有的$\rm M$原子的数目是                。

③当$\rm M$代表$\rm K$时，晶胞边长为$\rm \textit a\ nm$，阿伏加德罗常数为$\textit{N}_{\text{A}}$。该晶体密度为                $\text{g}\cdot \text{c}{{\text{m}}^{\text{-3}}}\rm (1\;\rm \text{nm}=1\times {{10}^{-7}}\;\rm \text{cm}\rm )$。

$\\rm 12$；$\\rm 12$；$\\dfrac{3348}{\\textit{N}_{\\text{A}}\\times\\textit{a}^{3}\\times10^{-21}}$

① 由晶胞结构可知，$\rm C_{60}$分子位于晶胞的顶点和面心，则与每个$\rm C_{60}$分子紧邻且等距的$\rm C_{60}$分子数目为$\rm 12$；

②某种$\rm C_{60}$的碱金属衍生物的化学式为$\rm M_{3}C_{60}$，该晶胞中$\rm C_{60}$分子的个数为$8\times \dfrac{1}{8}+6\times \dfrac{1}{2}=4$，则每个晶胞中含有的$\rm M$原子的数目是$4\times 3=12$；

③当$\rm M$代表$\rm K$，晶胞边长为$\rm \textit a\ nm$，阿伏加德罗常数为$\rm \textit N_{A}$时，该晶体密度为：$\dfrac{4\text{M}}{\left( \textit{a}\times10^{-7}\right)^{3}\cdot\textit{N}_{\text{A}}}=\dfrac{3348}{\textit{N}_{\text{A}}\times\textit{a}^{3}\times10^{-21}}\ \text{g/c}\text{m}^{3}$。