半正多面体$(semiregularsolid)$亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，半正多面体有且只有$13$种．最早用于$1970$年世界杯比赛的足球就可以近似看作是由$12$个正五边形和$20$个正六边形组成的半正面体，半正多面体体现了数学的对称美．如图所示的二十四等边体就是一种半正多面体，它由$8$个正三角形和$6$个正方形围成，它是通过对正方体进行八次切截而得到的．若这个二十四等边体的棱长都为$2$，则下列结论正确的是$(\qquad)$．

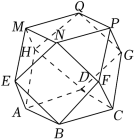
$MQ$与平面$AEMH$不可能垂直

异面直线$BC$和$EA$所成角为$60{}^\\circ $

该二十四等边体的体积为$\\dfrac{40\\sqrt{2}}{3}$

该二十四等边体外接球的表面积为$18\\pi $

对于$\rm A$，若$MQ\perp $平面$AEMH$，

$\because MH\subset $平面$AEMH$，

$\therefore MQ\perp MH$，

又$\because \triangle MQH$为等边三角形，

$\therefore \angle QMH=60{}^\circ $，这与$MQ\perp MH$矛盾，故$MQ$与平面$AEMH$不可能垂直，

$\therefore \rm A$正确；

对于$\rm B$，$\because BC//AD$，

$\therefore $ 异面直线$BC$和$EA$所成的角即为直线$AD$和$EA$所成的角，设角$\angle EAD=\theta $，在正六边形$ADGPNE$中，可得$\theta =120{}^\circ $，

$\therefore $ 异面直线$BC$和$EA$所成角为$60{}^\circ $，

$\therefore \rm B$正确；

对于$\rm C$，补全八个角构成一个棱长为$2\sqrt{2}$的一个正方体，则该正方体的体积为$V={{(2\sqrt{2})}^{3}}=16\sqrt{2}$，其中每个小三棱锥的体积为${{V}_{1}}=\dfrac{1}{3}\times \dfrac{1}{2}\times \sqrt{2}\times \sqrt{2}\times \sqrt{2}=\dfrac{\sqrt{2}}{3}$，

$\therefore $ 该二十四面体的体积为$16\sqrt{2}-8\times \dfrac{\sqrt{2}}{3}=\dfrac{40\sqrt{2}}{3}$，

$\therefore \rm C$正确；

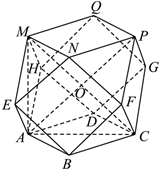
对于$\rm D$，取正方形$ACPM$对角线的交点为$O$，即为该二十四面体的外接球的球心，

其半径为$R=\dfrac{1}{2}\sqrt{A{{C}^{2}}+A{{M}^{2}}}=\dfrac{1}{2}\sqrt{{{(2\sqrt{2})}^{2}}+{{(2\sqrt{2})}^{2}}}=2$，

$\therefore $ 该二十四面体的外接球的表面积为$S=4\pi {{R}^{2}}=4\pi \times {{2}^{2}}=16\pi $，

$\therefore \rm D$不正确．

故选：$\rm ABC$