如图，长方体$ABCD-ABCD$的底面$ABCD$是正方形，点$E$在棱$AA_1$上，$BE⊥EC_1$$.$

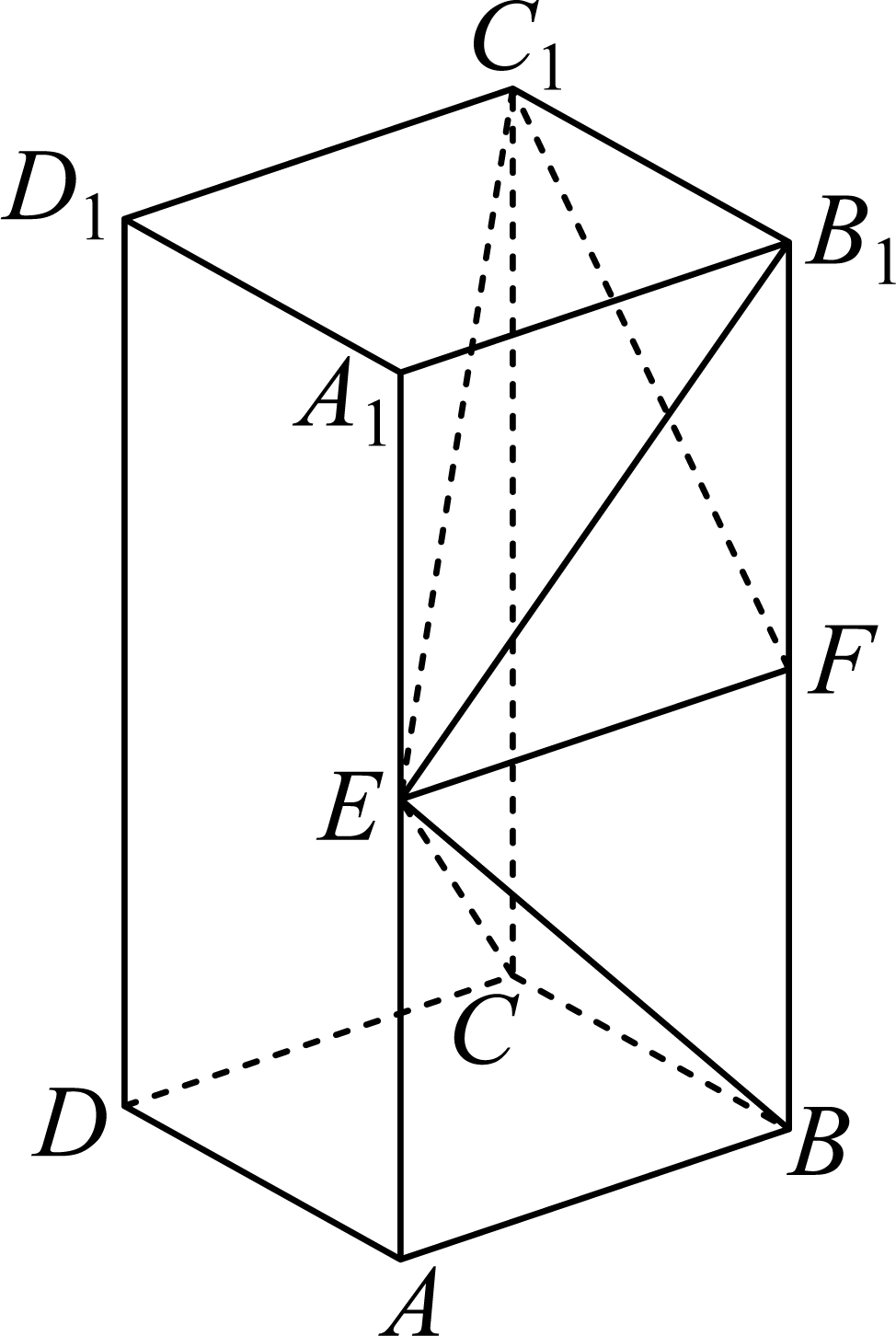
$(1)$证明$:$ $BE⊥$平面$EB_1C_1$

$(2)$若$AA_1$$=2$，$AB=1$，求四棱锥$E-BB_1C_1C$的体积$.$

$(1)$证明见解析

$(2)$$\\dfrac{2}{3}.$

$(1)$

证明：由长方体的性质可知，${{B}_{1}}{{C}_{1}}\perp $平面$ABB_1A\because BE\subset ABB_1A_1$

$\therefore BE\perp {{B}_{1}}{{C}_{1}}\because BE\perp E{{C}_{1}}$

$\because {{B}_{1}}{{C}_{1}},E{{C}_{1}}\subset $平面$E{{B}_{1}}{{C}_{1}}$，

$\therefore {{B}_{1}}{{C}_{1}}\cap E{{C}_{1}}={{C}_{1}}$

$∴$$BE$$⊥$平面$E{{B}_{1}}{{C}_{1}}$ $.$

$(2)$取棱$BB_1$的中点$F$，连接$EF$、$CF$

则$EF//AB,EF=AB=2$

由$(1)$知，$\angle BEB_1=90{}^\circ $由题设可知，$Rt\triangle ABE\overset{\Large∽}{=} Rt\triangle ABE$

$\therefore \angle AEB=\angle A_1EB_1=45{}^\circ \therefore AE=AB=1,AA_1=2AE=2$

$∵$在长方体 $ABCD-A_1B_1C_1D_1$中，$AA_1//$平面$BB_1C_1C,E\in AA_1$

$AB\perp BB_1C_1C$

$∴$点$E$到平面$BB_1C_1C$的距离$d=EF=AB=2$

$∴$四棱锥$E-BB_1C_1C$的体积 $V=\dfrac{1}{3}\cdot d\cdot {{S}_{B{{B_1}}{{C}_{1}}C}}=\dfrac{1}{3}\times 1\times 2\times 1=\dfrac{2}{3}.$