（$24-25$高二上$·$上海宝山$·$月考）如图，在棱长为$1$的正方体$ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$中，$EF$及$G$分别为棱$B{{B}_{1}},D{{D}_{1}}$和$C{{C}_{1}}$的中点．

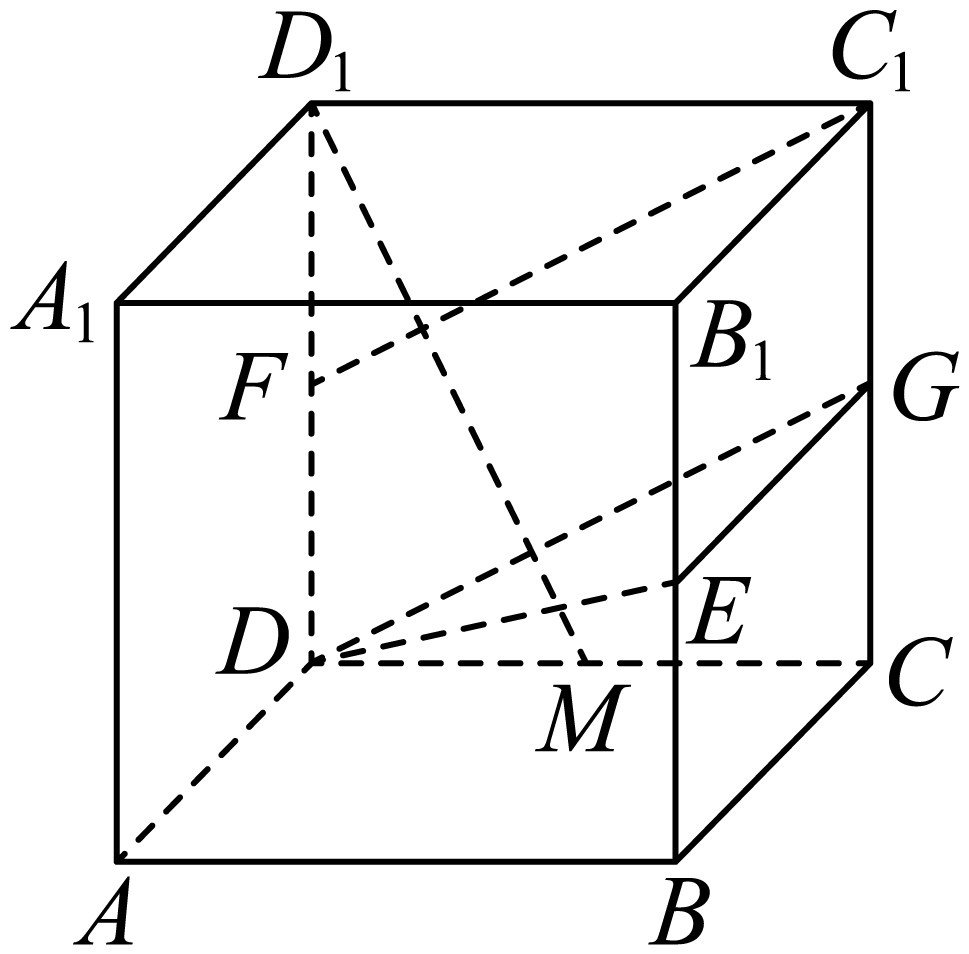
$(1)$求证：${{C}_{1}}F//$平面$DEG$；

$(2)$若$M$为棱$CD$的中点，求证：${{D}_{1}}M\perp $平面$DEG$．

$(1)$证明见解析；

$(2)$证明见解析$.$

$(1)$在正方体$ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$中，$E$，$F$，$G$分别为棱$B{{B}_{1}},D{{D}_{1}}$和$C{{C}_{1}}$的中点，

$DF//{{C}_{1}}G$，且$DF={{C}_{1}}G$，则四边形$DG{{C}_{1}}F$是平行四边形，${{C}_{1}}F//DG$，

而$DG\subset $平面$DEG,{{C}_{1}}F\not\subset $平面$DEG$，

$\therefore {{C}_{1}}F//$平面$DEG.$

$(2)$在正方体$ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$中，$BC\perp $平面$CD{{D}_{1}}{{C}_{1}}$，${{D}_{1}}M\subset $面$CD{{D}_{1}}{{C}_{1}}$，则$BC\perp {{D}_{1}}M$，

由$E,G$是正方形$BC{{C}_{1}}{{B}_{1}}$边$B{{B}_{1}},C{{C}_{1}}$的中点，得$BC//EG$，则${{D}_{1}}M\perp EG$，

$M$为棱$CD$的中点，在正方形$CD{{D}_{1}}{{C}_{1}}$中，$\tan \angle D{{D}_{1}}M=\dfrac{DM}{D{{D}_{1}}}=\dfrac{1}{2}=\dfrac{CG}{CD}=\tan \angle CDG$，

则$\angle D{{D}_{1}}M=\angle CDG$，即$\angle {{D}_{1}}MD+\angle CDG=\angle {{D}_{1}}MD+\angle D{{D}_{1}}M=\dfrac{\pi}{2}$，则${{D}_{1}}M\perp DG$，

又$EG\cap DG=G,EG,DG\subset $平面$DEG$，

$\therefore {{D}_{1}}M\perp $平面$DEG.$