（$24-25$高二上$·$上海$·$期中）如图，已知圆锥的顶点为$P$，底面圆$O$的直径$AB$长为$8$，点$C$是圆$O$上一点，$\angle BOC=45{}^\circ $， 点$D$是劣弧$AC$上的一点， 平面$PCD\cap $平面$PAB=l$， 且$l\text{//}AB$$.$

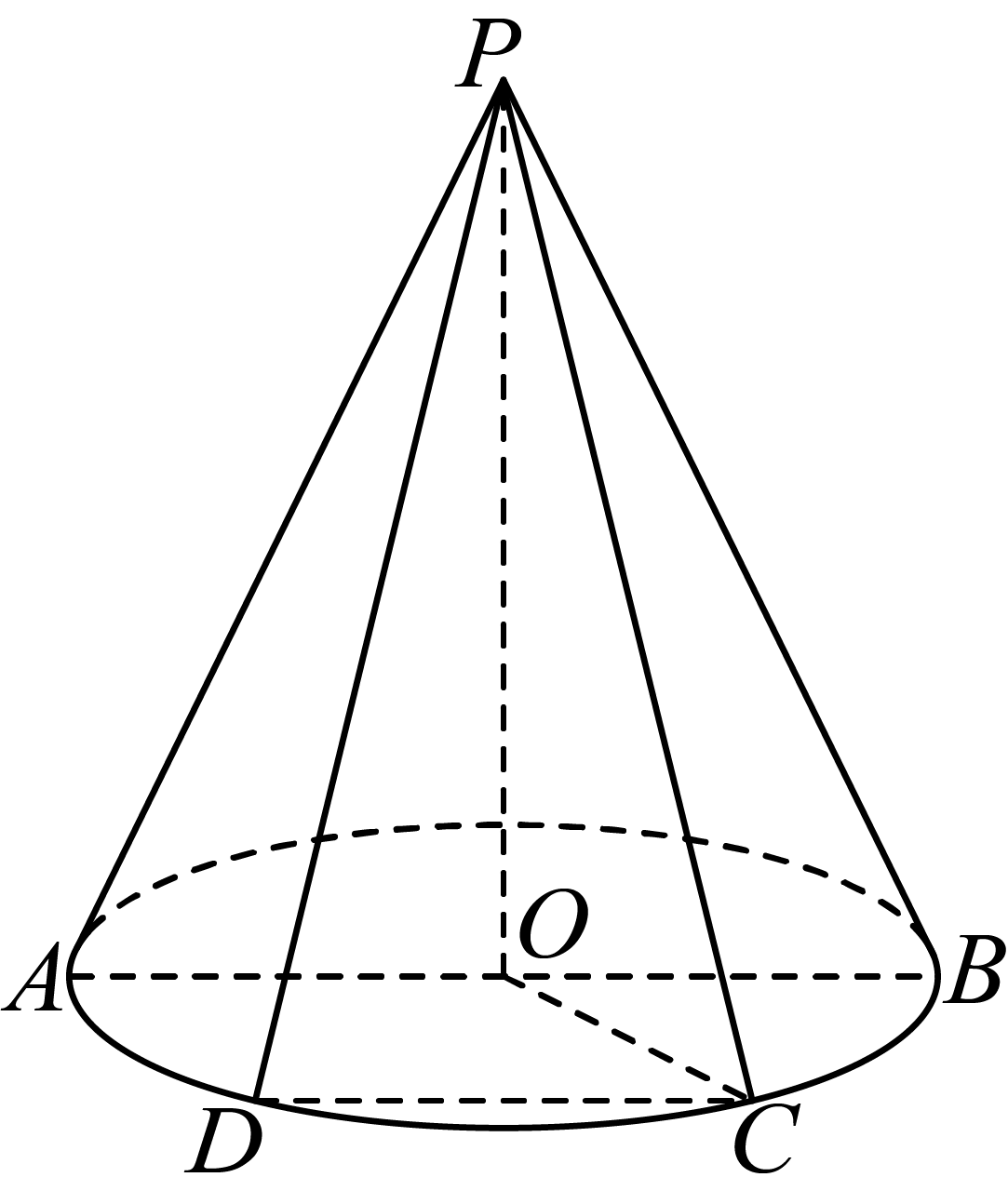
$(1)$证明：$OC\perp PD$$.$

$(2)$当三棱锥$P-OCD$的体积为$\dfrac{64}{7}$时，求点$O$到平面$PCD$的距离$.$

$(1)$证明见解析

$(2)$$\\dfrac{24}{11}$

$(1)$

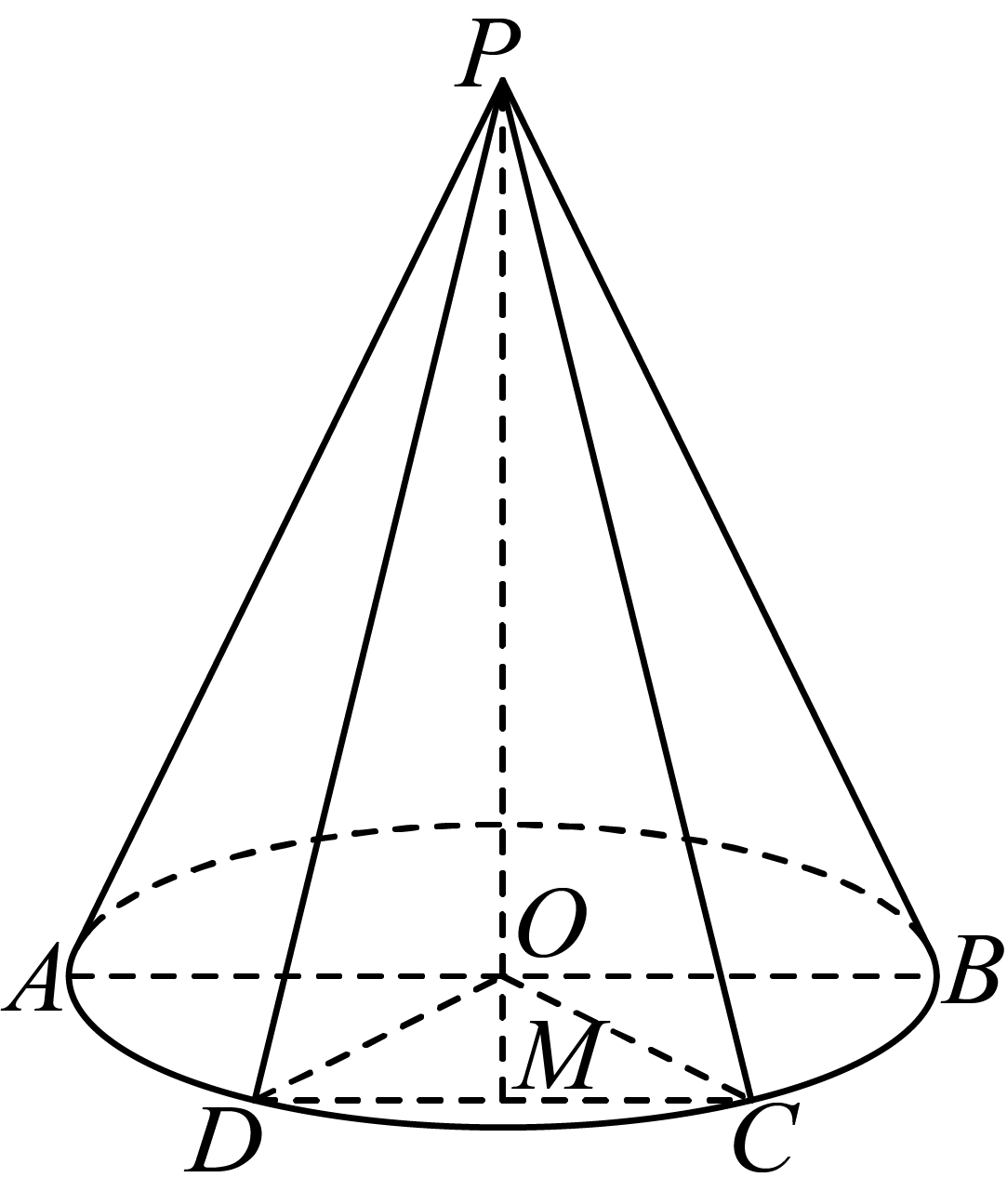
如图，由已知平面$PCD\cap $平面$PAB=l$， 且$l\text{//}AB$，

因$AB\not\subset $平面$PCD$，$l\subset $平面$PCD$，

则直线$AB\text{//}$平面$PCD$，

又$AB\subset $平面$ABCD$，且平面$ABCD\cap $平面$PCD=CD$，

则$AB\text{//}CD$，

又$\angle BOC=45{}^\circ $，

$\therefore \angle OCD=\angle ODC=45{}^\circ $，

即$\triangle OCD$为等腰直角三角形，

即$OC\perp OD$，

又由圆锥性质可得$PO\perp $平面$COD$,因$OC\subset $平面$COD$,则$PO\perp OC$，

因$OD\cap PO=O$，且$OD$，$PO\subset $平面$POD$，

故$OC\perp $平面$POD$，

又$P D \subset$平面$POD$，

故$OC\perp PD$；

$(2)$

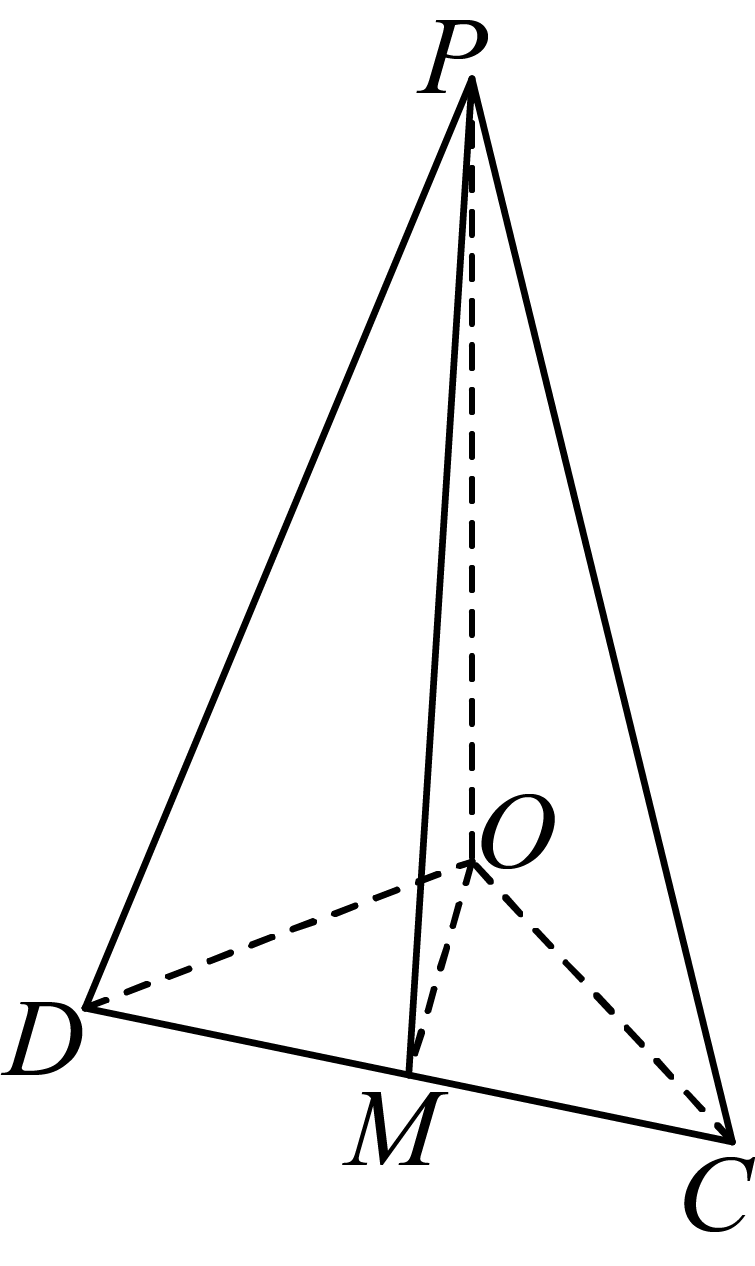
由已知圆$O$的直径$AB$长为$8$，则$OC=OD=4$，

由$(1)$得$CD=4\sqrt{2}$，${{S}_{\triangle OCD}}=\dfrac{1}{2}OC\cdot OD=8$，

由三棱锥$P-OCD$的体积$V=\dfrac{1}{3}{{S}_{\triangle OCD}}\cdot PO=\dfrac{8}{3}PO=\dfrac{64}{7}$，解得$PO=\dfrac{24}{7}$，

如图，取$CD$中点$M$，连接$OM$，$PM$，则$DC\perp OM$,因$PO\perp $平面$COD$,

因$DC\subset $平面$COD$,则$PO\perp DC$,因$PO\cap OM=O,PO,OM\subset $平面$POM$，则$D C \perp$平面$POM$,

又$PM\subset $平面$POM$，故$DC\perp PM$$.$

因$OM=2\sqrt{2}$，$PM=\sqrt{P{{O}^{2}}+O{{M}^{2}}}=\sqrt{{{\left(\dfrac{24}{7}\right)}^{2}}+{{(2\sqrt{2})}^{2}}}=\dfrac{22\sqrt{2}}{7}$，

$\therefore {{S}_{\triangle PCD}}=\dfrac{1}{2}CD\cdot PM=\dfrac{1}{2}\times 4\sqrt{2}\times \dfrac{22\sqrt{2}}{7}=\dfrac{88}{7}$，设点$O$到平面$PCD$的距离为$d$，

由$V=\dfrac{1}{3}{{S}_{\triangle PCD}}\cdot d=\dfrac{88}{21}d=\dfrac{64}{7}$，解得$d=\dfrac{24}{11}$$.$

即点$O$到平面$PCD$的距离为$\dfrac{24}{11}$$.$