如图，正方体$ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$中，$P$为棱$A{{A}_{1}}$上一点；

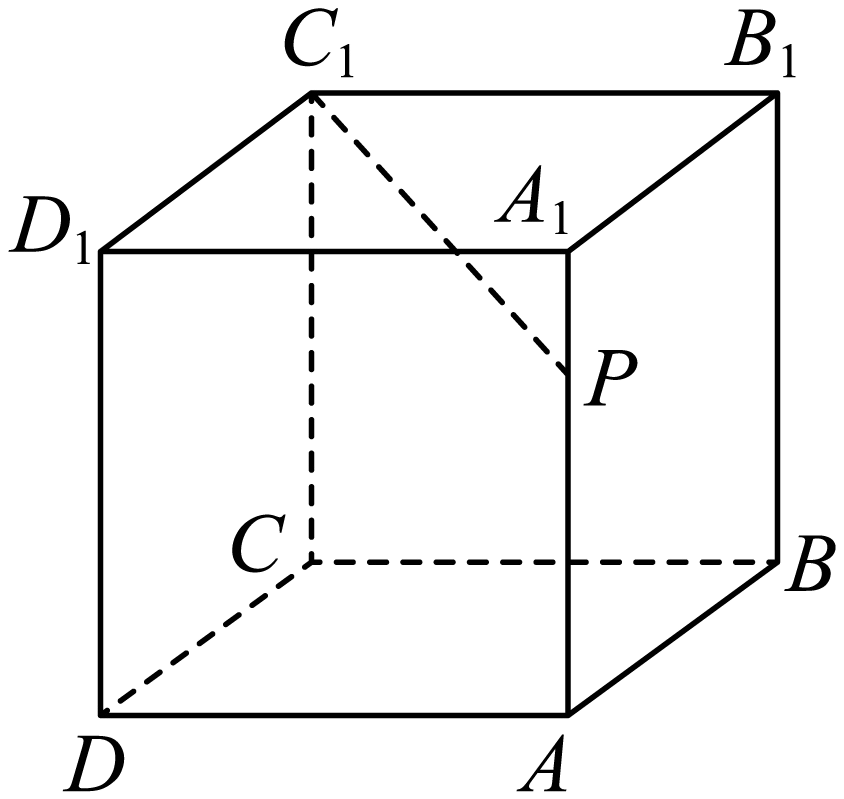
$(1)$试过点$P$在平面$AD{{D}_{1}}{{A}_{1}}$上作一条直线$PQ$，使得$PQ\perp {{C}_{1}}P$，写出作法并说明理由；

$(2)$若$P$为棱$A{{A}_{1}}$的中点，$Q$为棱$AD$上一点，且$PQ\perp {{C}_{1}}P$，求异面直线$PQ$与${{C}_{1}}D$所成的角$.$

$(1)$作法见解析，理由见解析

$(2)$$\\arccos \\dfrac{\\sqrt{10}}{5}$

$(1)$解：连接$P{{D}_{1}}$，

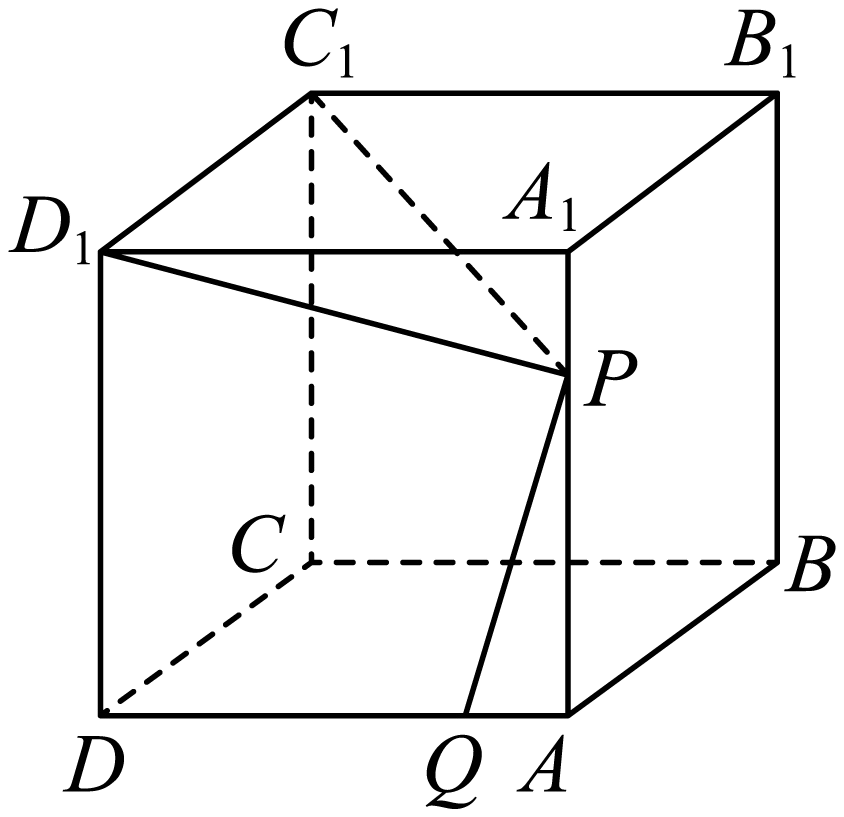
过点$P$在平面$A A_1D_1D$内作$PQ\perp P{{D}_{1}}$，则$PQ\perp P{{C}_{1}}$，理由如下：

在正方体$ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$中，${{C}_{1}}{{D}_{1}}\perp $平面$A A_1D_1D$，$PQ\subset $平面$A A_1D_1D$，则$PQ\perp {{C}_{1}}{{D}_{1}}$，

又$\because PQ\perp P{{D}_{1}}$，$P{{C}_{1}}\cap P{{D}_{1}}=P$，$P{{C}_{1}}$、$P{{D}_{1}}\subset $平面$P{{C}_{1}}{{D}_{1}}$，

$\therefore $ ，$PQ\perp $平面$P{{C}_{1}}{{D}_{1}}$，

$\because P{{C}_{1}}\subset $平面$P{{C}_{1}}{{D}_{1}}$，

$\therefore $ ，$PQ\perp P{{C}_{1}}$$.$

$(2)$解：设正方体$ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$的棱长为$4$，设$AQ=a\left( 0\le a\le 4 \right)$，则$DQ=4-a$，

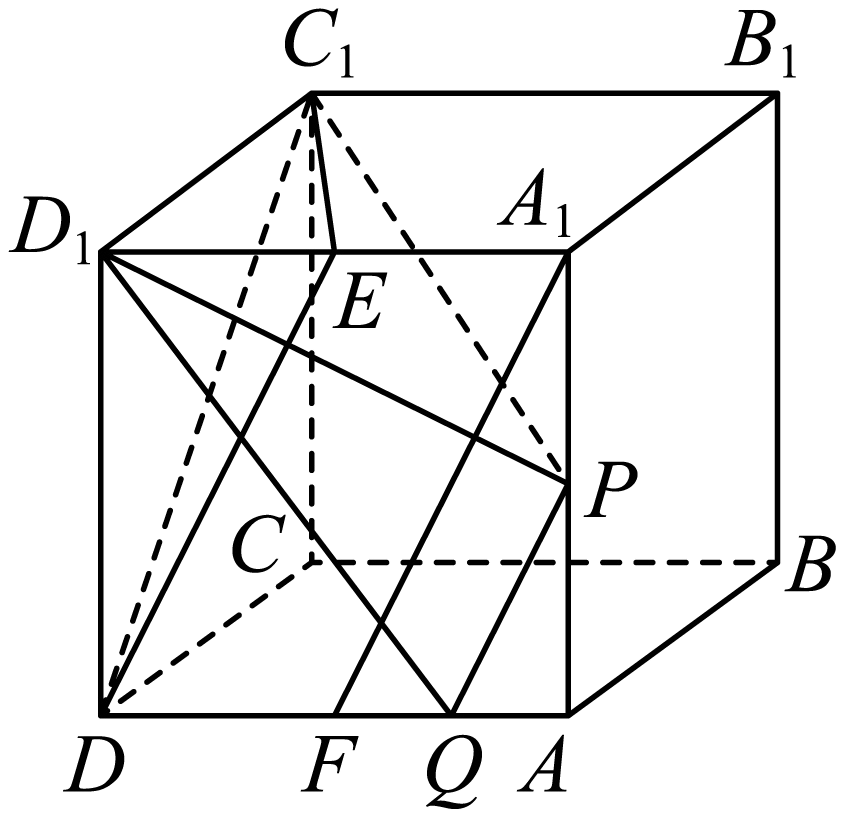
由$(1)$可知，若$P{{C}_{1}}\perp PQ$，则$P{{D}_{1}}\perp PQ$，

由勾股定理可得$P{{D}_{1}}=\sqrt{{{A}_{1}}{\rm D}_{1}^{2}+{{A}_{1}}{{P}^{2}}}=\sqrt{{{4}^{2}}+{{2}^{2}}}=2\sqrt{5}$，

同理可得$PQ=\sqrt{{{a}^{2}}+4}$，${{D}_{1}}Q=\sqrt{{{\left( 4-a \right)}^{2}}+16}=\sqrt{{{a}^{2}}-8a+32}$，

$\therefore $ ，$P{\rm D}_{1}^{2}+P{{Q}^{2}}={{D}_{1}}{{Q}^{2}}$，即$20+{{a}^{2}}+4={{a}^{2}}-8a+32$，解得$a=1$，即$AQ=1$，

分别取线段$AD$、${{A}_{1}}{{D}_{1}}$的中点$F$、$E$，连接$DE$、${{A}_{1}}F$，则$AF=2$，

$\therefore $ ，$Q$为$AF$的中点，又$\because P$为$A{{A}_{1}}$的中点，

$\therefore $ ，$PQ\text{//}{{A}_{1}}F$，

$\because AD\text{//}{{A}_{1}}{{D}_{1}}$且$AD={{A}_{1}}{{D}_{1}}$，$F$、$E$分别为$AD$、${{A}_{1}}{{D}_{1}}$的中点，

$\therefore $ ，${{A}_{1}}E\text{//}DF$且${{A}_{1}}E=DF$，

故四边形${{A}_{1}}EDF$为平行四边形，则$DE\text{//}{{A}_{1}}F$，

$\therefore $ ，$PQ\text{//}DE$，

$\therefore $ ，异面直线$PQ$与${{C}_{1}}D$所成的角为$\angle {{C}_{1}}DE$，

在$\triangle {{C}_{1}}DE$中，由勾股定理可得$DE=\sqrt{D{\rm D}_{1}^{2}+{{D}_{1}}{{E}^{2}}}=\sqrt{{{4}^{2}}+{{2}^{2}}}=2\sqrt{5}$，

同理可得${{C}_{1}}E=2\sqrt{5}$，${{C}_{1}}D=4\sqrt{2}$，

由余弦定理可得$\cos \angle {{C}_{1}}DE=\dfrac{{{C}_{1}}{{D}^{2}}+D{{E}^{2}}-{{C}_{1}}{{E}^{2}}}{2{{C}_{1}}D\cdot DE}=\dfrac{32+20-20}{2\times 4\sqrt{2}\times 2\sqrt{5}}=\dfrac{\sqrt{10}}{5}$,

因此，异面直线$PQ$与${{C}_{1}}D$所成的角为$\arccos \dfrac{\sqrt{10}}{5}$$.$