如图，在棱长为$2$的正方体$ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$中，已知$N$，$Q$分别是棱$A{{A}_{1}}$，$C{{C}_{1}}$的中点，$M$，$P$分别是棱${{D}_{1}}{{C}_{1}}$，$BC$上的动点，下列结论正确的是$(\qquad)$．

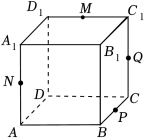
四面体$ADPM$的体积为定值

不存在动点$M$，$P$，使得$PM\\perp NQ$

直线$CM$与平面${{A}_{1}}{{B}_{1}}CD$所成角的范围是$\\left[\\dfrac{\\pi }{6},\\dfrac{\\pi }{4}\\right]$

若$M$，$P$分别是棱${{D}_{1}}{{C}_{1}}$，$BC$的中点，由平面$MNQ$分割该正方体，其中截面$MNQ$上方的部分为几何体$\\Omega $，某球能够被整体放入几何体$\\Omega $，则该球半径的最大值为$\\dfrac{3-\\sqrt{3}}{2}$

对于$\rm A$，${{V}_{ADPM}}={{V}_{M-ADP}}=\dfrac{1}{3}{{S}_{\triangle ADP}}\cdot D{{D}_{1}}=\dfrac{1}{3}\times \dfrac{1}{2}\times 2\times 2\times 2=\dfrac{4}{3}$，$\rm A$正确；

对于$\rm B$，连接$AC$，$BD$相交于$O$，当$P$是棱$BC$上的动点时，

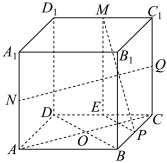
过$P$作$PE//BD$交$DC$于$E$，过$E$作$EM//D{{D}_{1}}$交$D{{D}_{1}}$于$M$，连接$MP$，

由于$AC\perp BD$，$PE//BD$，故$PE\perp AC$，

由$EM//D{{D}_{1}}D{{D}_{1}}\perp $平面$ABCD$，

故$EM\perp $平面$ABCD$，$AC\subset $平面$ABCD$，

故$EM\perp AC$，$EM\cap{E}P=E$，$EM$，$EP\subset $平面$EMP$，$PM\subset $平面$EMP$，

故$AC\perp PM$，

由于$N$，$Q$分别是棱$A{{A}_{1}}$，的中点，

$\therefore NQ//AC$，

$\therefore NQ\perp PM$，故$\rm B$错误； 

对于$\rm C$，由于$CD\perp $平面$AD{{D}_{1}}{{A}_{1}}$，$A{{D}_{1}}\subset $平面$AD{{D}_{1}}{{A}_{1}}$，故$A{{D}_{1}}\perp CD$，

又$A{{D}_{1}}\perp {{A}_{1}}D$，$CD\cap{{{A}_{1}}}D=D$，$CD$，${{A}_{1}}D\subset $平面${{A}_{1}}DC{{B}_{1}}$，

故$A{{D}_{1}}\perp $平面${{A}_{1}}DC{{B}_{1}}$，

故${{D}_{1}}$到平面${{A}_{1}}DC{{B}_{1}}$的距离为$\dfrac{1}{2}{{D}_{1}}A=\sqrt{2}$，

又${{D}_{1}}{{C}_{1}}$$\not\subset$平面${{A}_{1}}DC{{B}_{1}}$，

故${{D}_{1}}{{C}_{1}}//$平面${{A}_{1}}DC{{B}_{1}}$，

因此$M$到平面${{A}_{1}}DC{{B}_{1}}$的距离与${{D}_{1}}$到平面${{A}_{1}}DC{{B}_{1}}$的距离相等，即距离为$d=\sqrt{2}$，

由于$C{{C}_{1}}=2$，$C{{D}_{1}}=2\sqrt{2}$，

$\therefore MC\in [2,2\sqrt{2}]$，

设直线$CM$与平面${{A}_{1}}{{B}_{1}}CD$为$\theta $，

则$\sin \theta =\dfrac{d}{CM}=\dfrac{\sqrt{2}}{CM}\in \left[\dfrac{1}{2},\dfrac{\sqrt{2}}{2}\right]$，

由于$\theta \in \left[0,\dfrac{\pi }{2}\right]$，

故$\theta \in \left[\dfrac{\pi }{6},\dfrac{\pi }{4}\right]$，$\rm C$正确； 

对于$\rm D$，$R$，$S$分别是棱${{A}_{1}}{{D}_{1}}$，$AB$的中点，点$Q$为$C{{C}_{1}}$中点时，平面$MNP$在正方体上的截面为正六边形$MRNSPQ$，

某球能够被整体放入$\Omega $，该球的半径最大时，是以${{B}_{1}}$为顶点，底面为正六边形$MRNSPQ$的正六棱锥的内切球，正六边形$MRNSPQ$的边长为$\sqrt{2}$，面积为$6\times \dfrac{1}{2}\times \sqrt{2}\times \sqrt{2}\times \dfrac{\sqrt{3}}{2}=3\sqrt{3}$，

正六棱锥${{B}_{1}}-MRNSPQ$，侧棱长$\sqrt{5}$，每个侧面面积为$\dfrac{3}{2}$，棱锥的高为$\sqrt{3}$，

设该球的半径为$R$，由体积法可得$\dfrac{1}{3}\times 3\sqrt{3}\times \sqrt{3}=\dfrac{1}{3}\left(3\sqrt{3}+6\times \dfrac{3}{2}\right)R$，

解得$R=\dfrac{3-\sqrt{3}}{2}$，$\rm D$正确．

故选：$\rm ACD$