如图，四棱锥${{P}-{ABCD}}$中，$BC//AD$，$AD=CD=2BC=2$，平面$PAD$$⊥$平面$PBC$$.$

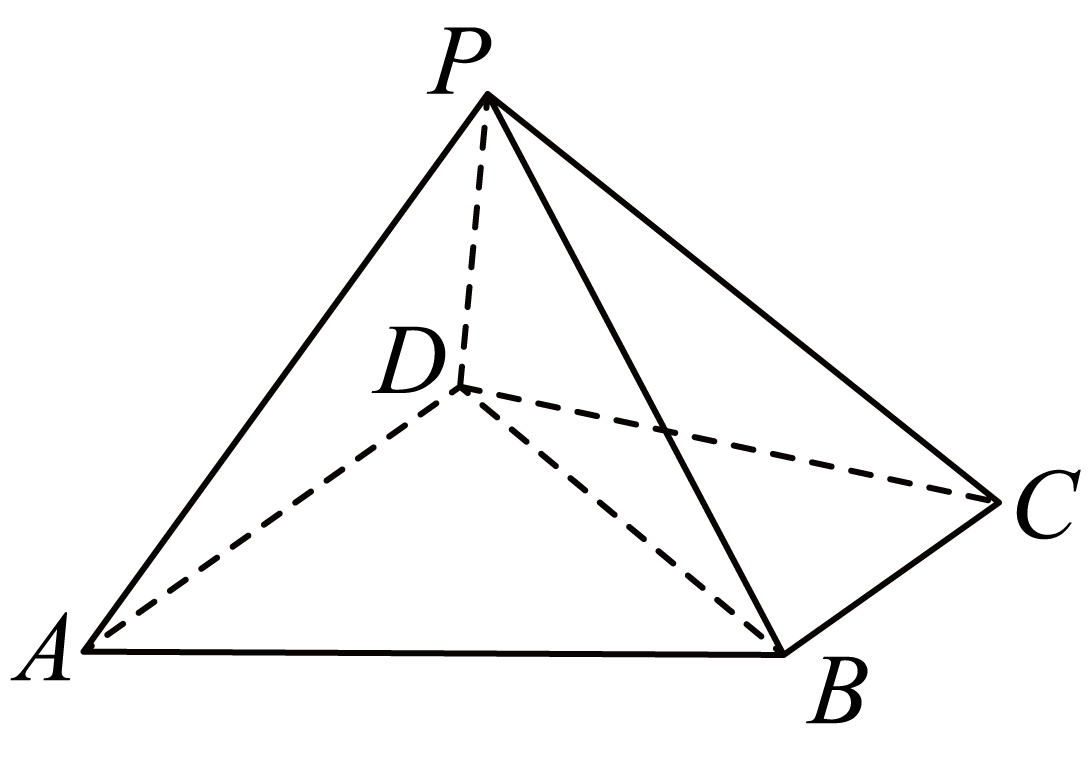
$(1)$若$PB\perp BC$，证明：$AP\perp BP$；

$(2)$若$PA\perp PC$，$\angle BCD=\dfrac{\pi }{3}$，求$PA$长度的取值范围$.$

$(1)$证明见解析；

$(2)$$(0,\\sqrt{3})\\cup (3,2\\sqrt{3})$

$(1)$设平面$ADP\cap $平面$BCP=l$，

$\because BC\parallel AD,AD\subset $平面$ADP,BC\not\subset $平面$ADP$，

$\therefore BC\parallel $平面$ADP$，

又$\because BC\subset $平面$BCP$，平面$ADP\cap $平面$BCP=l$，

$\therefore BC\parallel l$，

$\because PB\perp BC,BC\parallel l$，

$\therefore PB\perp l$，

又$\because $平面$ADP\perp $平面$BCP$，平面$ADP\cap $平面$BCP=l,PB\subset $平面$BCP$，

$\therefore PB\perp $平面$ADP$$.$

又$\because AP\subset $平面$ADP$，

$\therefore PB\perp AP$即$AP\perp BP$$.$

$(2)$在$\triangle BCD$中由余弦定理可得$BD=\sqrt{3}$，则有$B{{D}^{2}}+B{{C}^{2}}=C{{D}^{2}}$,

$\therefore \angle CBD=\dfrac{\pi}{2},$即$DB\perp BC$$.$

又$\because BC//AD\therefore DB\perp A D.$

以点$D$为原点，以$DA,DB$，平面$ABCD$的垂线所在直线分别为$x,y,z$轴，建立如图坐标系，则$A\left( 2,0,0 \right),B\left( 0,\sqrt{3},0 \right),C\left( -1,\sqrt{3},0 \right)$，

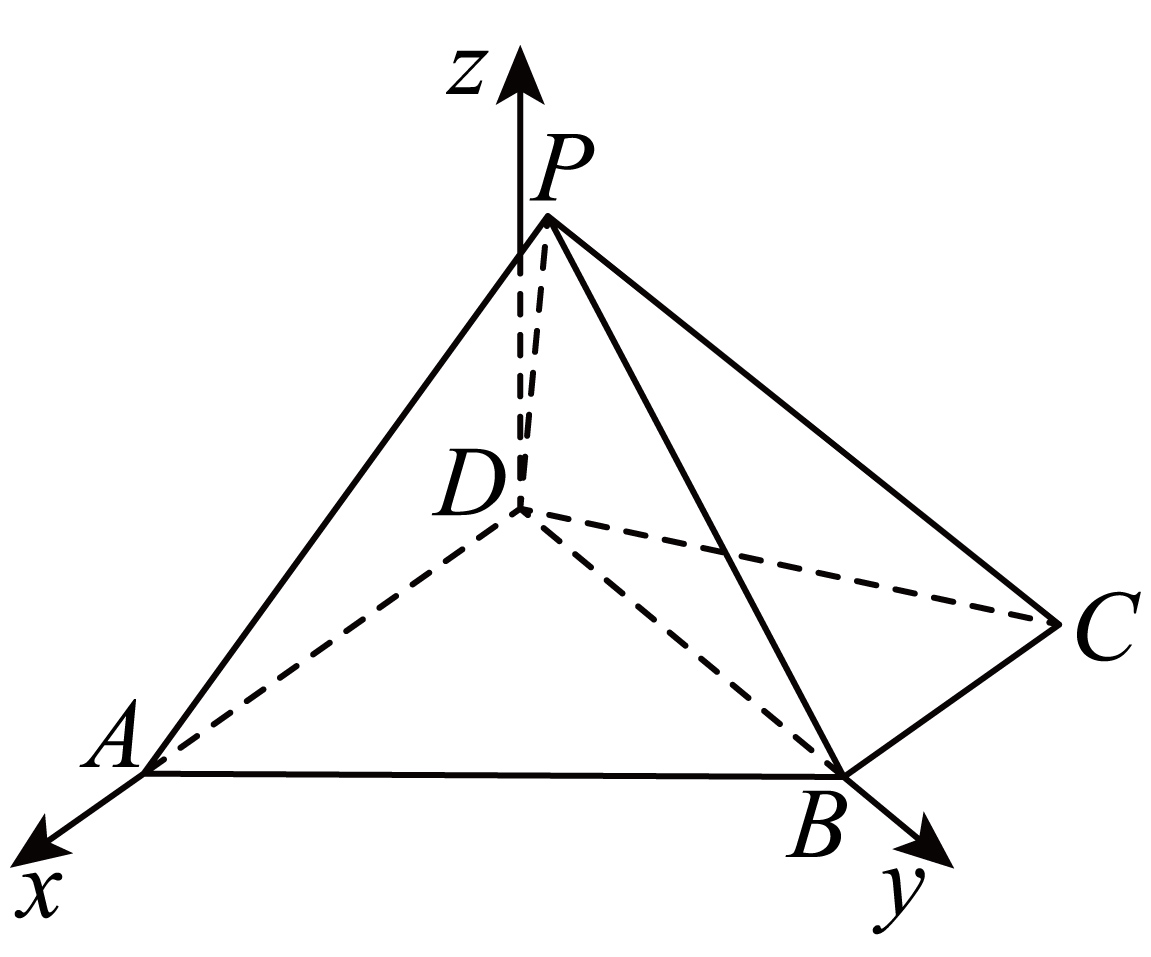
设$P\left( a,b,c \right)$，则$\overrightarrow{DP}=\left( a,b,c \right),\overrightarrow{DA}=\left( 2,0,0 \right)$,

设平面$PAD$的一个法向量为${{\boldsymbol{n}}_{1}}=\left( x,y,z \right)$，

则$\begin{cases} \boldsymbol{{n_1}}\cdot \overrightarrow{DA}=0 \\ \boldsymbol{{n_1}}\cdot \overrightarrow{DP}=0 \\ \end{cases}$，即$\begin{cases} 2x=0 \\ ax+by+cz=0 \\ \end{cases}$，令$y=c$，则$\boldsymbol{{n_1}}=\left( 0,c,-b \right)$$.$

同理可求平面$PBC$的一个法向量为$\boldsymbol{{n_2}}=\left( 0,c,\sqrt{3}-b \right)$，

由于平面$PAD\perp $平面$PBC$，则$\overrightarrow{n_{1}} \cdot \overrightarrow{n_{2}}=0$，故${{c}^{2}}+b\left( b-\sqrt{3} \right)=0,$则$b\in \left( 0,\sqrt{3} \right)$$.$

又$\because PA\perp PC$，$\overrightarrow{PA}=\left( 2-a,-b,-c \right),\overrightarrow{PC}=\left( -1-a,\sqrt{3}-b,-c \right)$，

$\therefore \overrightarrow{PA}\cdot \overrightarrow{PC}=\left( a-2 \right)\left( a+1 \right)+b\left( b-\sqrt{3} \right)+{{c}^{2}}=0$，解得$a=2$或$-1$$.$

若$a=2$，则$PA=\sqrt{{{b}^{2}}+{{c}^{2}}}=\sqrt{\sqrt{3}b}\in \left( 0,\sqrt{3} \right)$$;$

若$a=-1$，则$PA=\sqrt{9+{{b}^{2}}+{{c}^{2}}}=\sqrt{9+\sqrt{3}b}\in \left( 3,2\sqrt{3} \right)$$.$

综上所述，$PA$长度的取值范围$\left( 0,\sqrt{3} \right)\cup \left( 3,2\sqrt{3} \right)$$.$