如图，在三棱柱$ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}$中，$M$，$N$分别为棱$BC$，$B_{1}C_{1}$的中点$.$

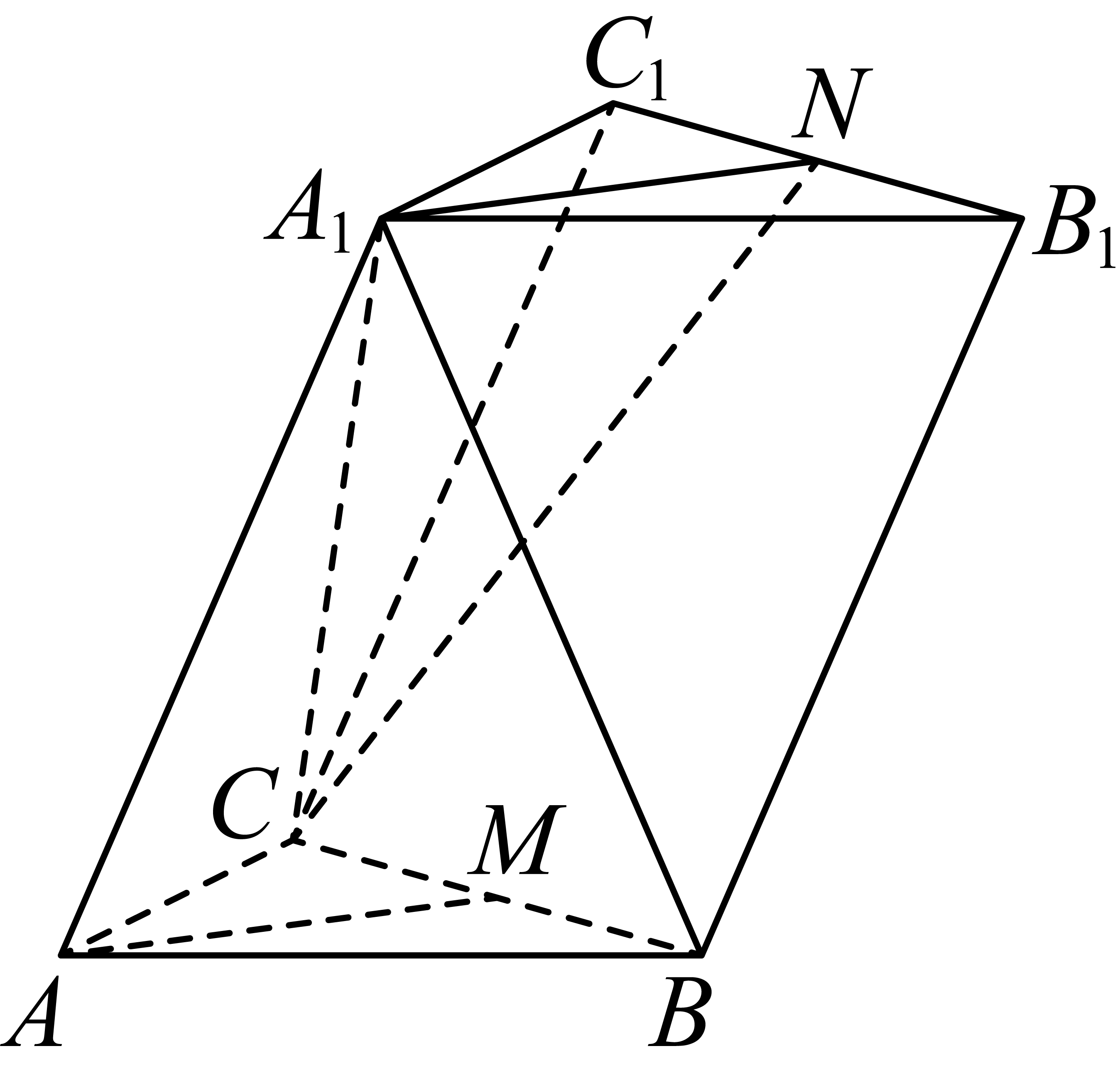
$(1)$求证$:$ $AM$∥平面${{A}_{1}}CN$；

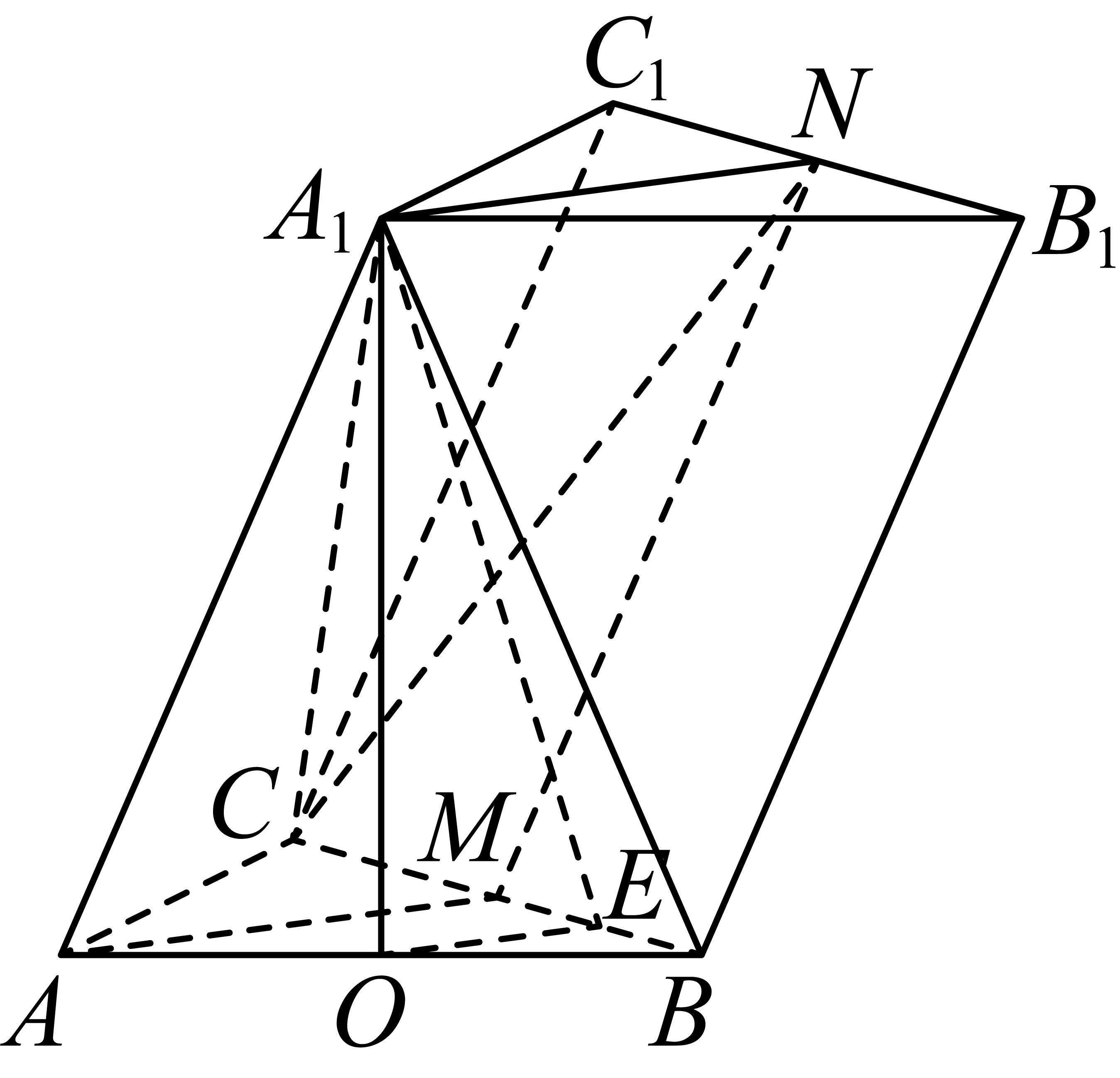
$(2)$若平面$ABC\perp $平面$A A_1 B_1 B$，$AB=AC$，${{A}_{1}}A={{A}_{1}}B$，点$E$满足$\overrightarrow{C E}=\lambda \overrightarrow{E B}$，且${{A}_{1}}E\perp {{B}_{1}}{{C}_{1}}$，求实数$\lambda $的值$.$

$(1)$证明见解析

$(2)3$

$(1)$连接$MN$，

$\because M$，$N$分别为棱$BC$，$B_{1}C_{1}$的中点，

$\therefore BM=\dfrac{1}{2}BC,{{B}_{1}}N=\dfrac{1}{2}{{B}_{1}}{{C}_{1}}$，

$\because BC$∥$B_{1}C_{1}$，$BC={{B}_{1}}{{C}_{1}}$，

$\therefore BM$∥${{B}_{1}}N$，$BM={{B}_{1}}N$，

$\therefore $ 四边形$B{{B}_{1}}NM$为平行四边形，

$\therefore MN$∥${{B}_{1}}B$，$MN={{B}_{1}}B$，又${{A}_{1}}A$∥${{B}_{1}}B$，${{A}_{1}}A={{B}_{1}}B$，

$\therefore {{A}_{1}}A$∥$MN$，${{A}_{1}}A=MN$，

$\therefore $ 四边形${{A}_{1}}AMN$为平行四边形，

$\therefore {{A}_{1}}N$∥$AM$，又$\because {{A}_{1}}N\subset $平面${{A}_{1}}CN$，$AM\not\subset$平面${{A}_{1}}CN$，

$\therefore AM$∥平面${{A}_{1}}CN$$.$

$(2)$解：取$AB$的中点$O$，连接${{A}_{1}}O$，

$\because {{A}_{1}}A={{A}_{1}}B$，

$\therefore {{A}_{1}}O\perp AB$，

$\because $ 平面$ABC\perp $平面$A A_1 B_1 B$，平面$ABC\cap $平面$A{{A}_{1}}{{B}_{1}}B=AB$，${{A}_{1}}O\subset $平面$A A_1 B_1 B$，

$\therefore {{A}_{1}}O\perp $平面$AB$  $C$.

$\because BC\subset $平面$ABC$，

$\therefore {{A}_{1}}O\perp BC$$.$

连接$OE$，

$\because B_{1}C_{1}$∥$BC$，${{A}_{1}}E\perp {{B}_{1}}{{C}_{1}}$，

$\therefore {{A}_{1}}E\perp BC$$.$

又${{A}_{1}}O\cap {{A}_{1}}E={{A}_{1}}$，${{A}_{1}}O,{{A}_{1}}E\subset $平面${{A}_{1}}OE$，

$\therefore BC\perp $平面${{A}_{1}}OE$$.$

$\because OE\subset $平面${{A}_{1}}OE$，

$\therefore BC\perp OE$$.$

又$\because AB=AC$，

$\therefore AM\perp BC$，

$\therefore OE$∥$AM$，

$\therefore E$为$MB$的中点，即$\overrightarrow{CE}=3\overrightarrow{EB}$，

$\therefore \lambda =3$$.$