已知一个正四面体$QPTR$和一个正八面体$AEFBHC$的棱长都是$a$（如图），把它们拼接起来，使它们一个表面完全重合，得到一个新多面体．

$(1)$求新多面体的表面积和体积；

$(2)$求正八面体$AEFBH$中二面角$A-BF-C$的大小．

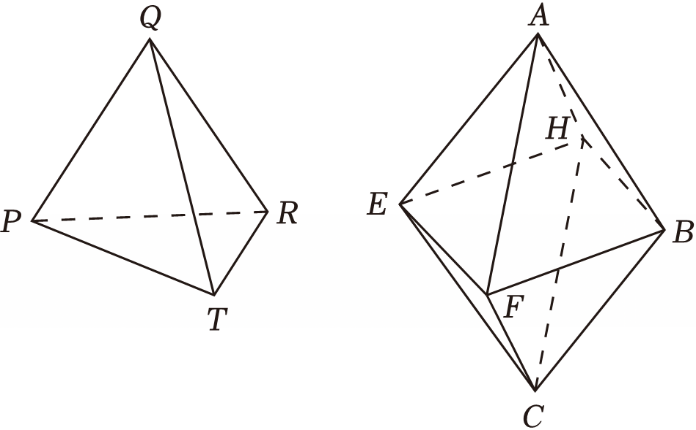
$(1)$$\\dfrac{5\\sqrt{3}{a}^{2}}{2}$，$\\dfrac{5\\sqrt{2}{a}^{3}}{12}$；$(2)$$\\arccos \\left(-\\dfrac{1}{3}\\right)$．

$(1)$由题意可知，组合体一共十个面，且十个面都是全等的等边三角形，且边长为$a$，

则表面积为$S=10\times \dfrac{\sqrt{3}}{4}{a}^{2}=\dfrac{5\sqrt{3}}{2}{a}^{2}$，

分别取$QR$、$PT$的中点$G$、$N$，连接$NQ$、$NR$、$NG$，如下图所示：

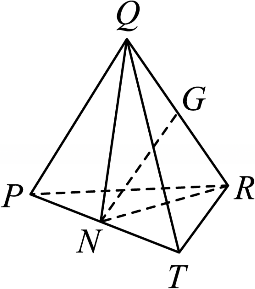
$\because PQ=QT$，$N$为$PT$的中点，则$QN\perp PT$且$NQ=\dfrac{\sqrt{3}}{2}a$，

同理可知$NQ\perp PT$且$NQ=\dfrac{\sqrt{3}}{2}a$，

$\because NQ\cap NR=N$，

$\therefore PT\perp$平面$NQR$，

$\because G$为$QR$的中点，则$NG\perp QR$，且$NG=\sqrt{N{Q}^{2}-Q{G}^{2}}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^{2}-\left(\dfrac{a}{2}\right)^{2}}=\dfrac{\sqrt{2}}{2}a$，

${S}_{\triangle NQR}=\dfrac{1}{2}QR\cdot NG=\dfrac{1}{2}\times a\times \dfrac{\sqrt{2}}{2}a=\dfrac{\sqrt{2}}{4}{a}^{2}$，

$\therefore $ 正四面体$Q-PRT$的体积为${V}_{1}=\dfrac{1}{3}{S}_{\triangle QNR}\cdot PT=\dfrac{1}{3}\times \dfrac{\sqrt{2}}{4}{a}^{2}\times a=\dfrac{\sqrt{2}}{12}{a}^{3}$；

如下图所示：

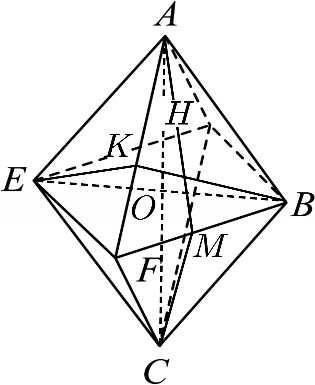
在正八面体中，连接$AC$交平面$EFBH$于点$O$，则$AO\perp$平面$EFBH$，

$\therefore {S}_{EFBG}={a}^{2}$，$AO=\sqrt{A{E}^{2}-O{E}^{2}}=\sqrt{{a}^{2}-\left(\dfrac{\sqrt{2}}{2}a\right)^{2}}=\dfrac{\sqrt{2}}{2}a$，

$\therefore $ 正八面体的体积为${V}_{2}=2\times \dfrac{1}{3}\times {S}_{EFBG}\times AO=2\times \dfrac{1}{3}\times {a}^{2}\times \dfrac{\sqrt{2}}{2}a=\dfrac{\sqrt{2}}{3}{a}^{3}$，

$\because $ 新多面体体积为原正四面体体积$V_{1}$与正八面体体积$V_{2}$之和，

$\therefore $ 新多面体的体积为$V={V}_{1}+{V}_{2}=\dfrac{5\sqrt{2}{a}^{3}}{12}$；

$(2)$如图，在正八面体中，取$BF$的中点为$M$，连接$AM$、$CM$，

$\because AB=AF$，$M$为$BF$的中点，则$AM\perp BF$，且$AM=\dfrac{\sqrt{3}}{2}a$，

同理可知$CM\perp BF$，且$CM=\dfrac{\sqrt{3}}{2}a$，

$\therefore \angle AMC$为二面角$A-BF-C$的平面角．

$\because AC=2AO=2\sqrt{A{E}^{2}-O{E}^{2}}=\sqrt{{a}^{2}-\left(\dfrac{\sqrt{2}}{2}a\right)^{2}}=\sqrt{2}a$，

由余弦定理得$\cos \angle ADC=\dfrac{M{A}^{2}+M{C}^{2}-A{C}^{2}}{2MA\cdot MC}=-\dfrac{1}{3}$，

故二面角$A-BF-C$的大小为$\arccos \left(-\dfrac{1}{3}\right)$；