中国古代数学的瑰宝《九章算术》中记载了一种称为“曲池”的几何体，该几何体是上、下底面均为扇环形的柱体（扇环是指圆环被扇形截得的部分）．现有一个如图所示的曲池，$AA_{1}$垂直于底面，$AA_{1}=5$，底面扇环所对的圆心角为$\dfrac{\pi }{2}$，弧$AD$的长度是弧$BC$长度的$3$倍，$CD=2$，则下列说法正确的是$(\qquad)$．

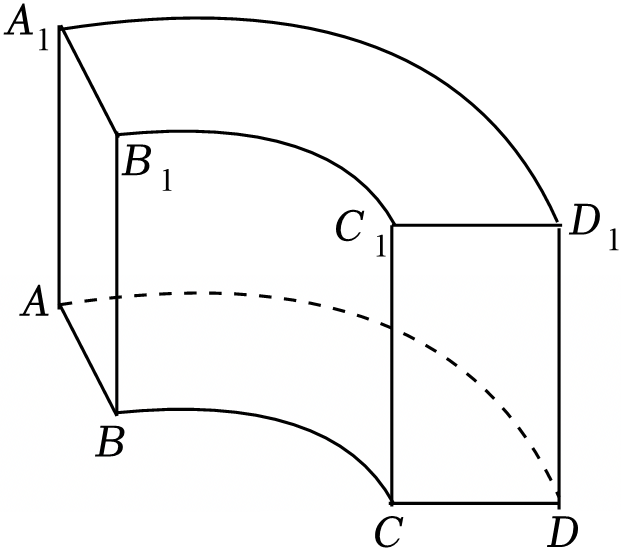
曲池的表面积为$10+7\\pi$

曲池的体积为$\\dfrac{10\\pi }{3}$

曲池的表面积为$20+14\\pi$

曲池的体积为$15\\pi$

如图，设弧$\rm BC$对应圆半径为$x$，则弧$\rm AD$对应圆半径为$x+2$．

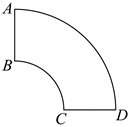
因弧$AD$的长度是弧$BC$长度的$3$倍，则$\dfrac{\dfrac{\pi }{2}(x+2)}{\dfrac{\pi }{2}x}=3\Rightarrow x=1$．

则$\overparen{BC}=\dfrac{\pi }{2}$，$\overparen{AD}=\dfrac{3\pi }{2}$，

$\therefore $ 底面扇环面积为：$\dfrac{1}{2}\times 2\times \left(\dfrac{\pi }{2}+\dfrac{3\pi }{2}\right)=2\pi$．

则曲池的体积为$2\pi \times 5=10\pi$，故$B$，$\rm D$错误；

曲面$BCC_{1}B_{1}$面积为$\dfrac{\pi }{2}\times 5=\dfrac{5\pi }{2}$，曲面$A_{1}ADD_{1}$面积为$\dfrac{3\pi }{2}\times 5=\dfrac{15\pi }{2}$，

底面面积为$2\pi \times 2=4\pi$，平面$AA_{1}B_{1}B$与平面$CC_{1}D_{1}D$面积之和为$2\times 5\times 2=20$．

则曲池的表面积为$\dfrac{5\pi }{2}+\dfrac{15\pi }{2}+4\pi +20=20+14\pi$．故$\rm A$错误，$\rm C$正确．

故选：$\rm C$