在棱长为$2$的正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中，$E$，$F$分别为棱$AB$，$AA_{1}$的中点，点$P$在对角线$A_{1}B$上，则$(\qquad)$．

$AP+D_{1}P$的最小值为$2\\sqrt{2+\\sqrt{2}}$

三棱锥$P-CEF$体积为$\\dfrac{1}{3}$

点$P$到平面$CEF$的距离为$\\dfrac{1}{6}$

四面体$BCEF$外接球的表面积为$14\\pi$

根据题意，可作图如下：

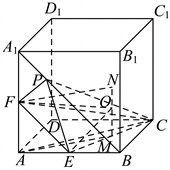
对于$\rm A$，在正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中，易知$A_{1}D_{1}\perp$平面$ABB_{1}A_{1}$，

$\because A_{1}B\subset$平面$ABB_{1}A_{1}$，

$\therefore A_{1}D_{1}\perp A_{1}B$，

将点$D_{1}$绕$A_{1}B$旋转得到$D_{1}$，使$A$，$P$，$D_{1}$共面，如下图：

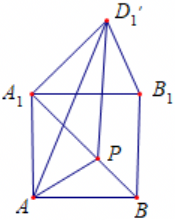
易知$AP+D_{1}P\geqslant AD_{1}$，在$\triangle $$AA_{1}D_{1}$中，易知$\angle AA_{1}D_{1}=135^\circ$，

由余弦定理，$A{\rm {D}}_{1}^{2}=A{\rm {A}}_{1}^{2}+{A}_{1}{\rm {D}}_{1}^{2}-2A{A}_{1}\cdot {A}_{1}{D}_{1}\cdot \cos \angle A{A}_{1}{D}_{1}=4+4-2\times 2\times 2\times \left(-\dfrac{\sqrt{2}}{2}\right)=8+4\sqrt{2}$，

则$A{D}_{1}=2\sqrt{2+\sqrt{2}}$，故$\rm A$正确；

对于$\rm B$，在正方体中$ABCD-A_{1}B_{1}C_{1}D_{1}$，$CB\perp AB$，$CB\perp$平面$ABB_{1}A_{1}$，

在三棱锥$P-CEF$中，以$\triangle PEF$为底面，则$CB$为其高，

$\because P\in A_{1}B$，易知$\triangle ABA_{1}$为等腰直角三角形，且$E$，$F$分别为$A_{1}A$，$AB$的中点，

$\therefore EF//A_{1}B$，且$P$到$EF$的距离为$\dfrac{1}{4}{A}_{1}B=\dfrac{1}{4}\times \sqrt{2}AB=\dfrac{\sqrt{2}}{2}$，

$\therefore {V}_{P-CEF}=\dfrac{1}{3}CB\cdot {S}_{\triangle PEF}=\dfrac{1}{3}\times 2\times \dfrac{1}{2}\times \sqrt{2}\times \dfrac{\sqrt{2}}{2}=\dfrac{1}{3}$，故$\rm B$正确；

对于$\rm C$，在${\rm Rt}\triangle BCE$中，易知$BE=1$，$BC=2$，则$CE=\sqrt{C{B}^{2}+B{E}^{2}}=\sqrt{5}$，

在${\rm Rt}\triangle AEF$中，易知$AE=AF=1$，则$EF=\sqrt{2}$，

在${\rm Rt}\triangle ACF$中，易知$AC=2\sqrt{2}$，$AF=1$，则$CF=\sqrt{A{F}^{2}+A{C}^{2}}=3$，

在$\triangle CEF$中，由余弦定理，$\cos \angle CEF=\dfrac{C{E}^{2}+E{F}^{2}-C{F}^{2}}{2\times CE\times EF}=-\dfrac{\sqrt{10}}{10}$，

则$\sin \angle CEF=\dfrac{3\sqrt{10}}{10}$，

$\therefore {S}_{\triangle CEF}=\dfrac{1}{2}EF\cdot CE\sin \angle CEF=\dfrac{3}{2}$，

点$P$到平面$CEF$的距离为$\dfrac{3{V}_{P-CEF}}{{S}_{\triangle CEF}}=\dfrac{3\times \dfrac{1}{3}}{\dfrac{3}{2}}=\dfrac{2}{3}$，

即点$P$到平面$CEF$的距离为$\dfrac{2}{3}$，故$\rm C$不正确；

对于$\rm D$，取$EC$的中点$M$，易知$M$为${\rm Rt}\triangle BCE$的外接圆圆心，连接$AM$，

作$NM//AA_{1}$，$FN//AM$，取$O\in MN$，连接$OE$，$OF$，如下图：

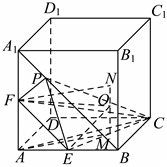
$\because NM//AA_{1}$，

$\therefore MN\perp$平面$BCE$，由$M$为$\rm{Rt}\triangle BCE$的外接圆圆心，

则可设$O$为三棱锥$F-BCE$的外接球球心，即$OE=OF=R$，

$\because FN//AM$，

$\therefore $ 易知四边形$AMNF$为矩形，则$AM=FN$，$MN\perp FN$，

在$\triangle AEM$中，由余弦定理得：$A{M}^{2}=A{E}^{2}+E{M}^{2}-2AE\cdot EM\cos \angle AEM=\dfrac{13}{4}$，

在${\rm Rt}\triangle BCE$中，$\cos \angle CEB=\dfrac{BE}{CE}=\dfrac{\sqrt{5}}{5}$，易知$\angle AEC=\pi -\angle CEB$，则$\cos \angle AEC=-\dfrac{\sqrt{5}}{5}$，

在${\rm Rt}\triangle MOE$中，$O{E}^{2}=M{E}^{2}+M{O}^{2},OM=\sqrt{O{E}^{2}-M{E}^{2}}=\sqrt{{R}^{2}-\dfrac{5}{4}}$，

在${\rm Rt}\triangle MOF$中，$OF^{2}=ON^{2}+FN^{2}$，$OF^{2}=FN^{2}+(1-OM)^{2}$，

则${R}^{2}=\dfrac{13}{4}+\left(1-\sqrt{{R}^{2}-\dfrac{5}{4}}\right)^{2}$，解得${R}^{2}=\dfrac{7}{2}$，则球的表面积为$S=4\pi R^{2}=12\pi$，故$\rm D$正确．

故选：$\rm ABD$