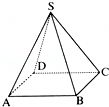
正棱锥$S-ABCD$的底面边长为$4$，高为$1$，求：

$(1)$棱锥的侧棱长和斜高；

$(2)$棱锥的表面积．

$(1)$棱锥的侧棱长为$3$，斜高为$\\sqrt{5}$；

$(2)$$16+8\\sqrt{5}$

$(1)$设$SO$为正四棱锥$S-ABCD$的高，则$SO=1$，

作$OM\perp BC$，则$M$为$BC$ 中点，

连结$OM$，$OB$，则$SO\perp OB$，$SO\perp OM$，

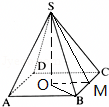
$BC=4$，$BM=2$，则$OM=2$，$OB=2\sqrt{2}$，

在$\rm{Rt}\triangle SOD$中，$SB=\sqrt{S{O}^{2}+O{B}^{2}}=\sqrt{1+8}=3$，

在$\rm{Rt}\triangle SOM$中，$SM=\sqrt{5}$，

$\therefore $棱锥的侧棱长为$3$，斜高为$\sqrt{5}$；

$(2)$棱锥的表面积：

$S={{S}_{ABCD}}+4{{S}_{\triangle SBC}}$

$=4\times 4+4\times \left(\dfrac{1}{2}\times 4\times \sqrt{5}\right)$

$=16+8\sqrt{5}$．