如图，正方体$ABCD-{A}{'}{B}{'}{C}{'}{D}{'}$的棱长为$a$，连接${A}{'}{C}{'}$，${A}{'}D$，${A}{'}B$，$BD$，$BC'$，${C}{'}D$，得到一个三棱锥.

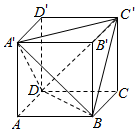
$(1)$求三棱锥${A}{'}-BC'D$的表面积与正方体的表面积的比值；
$(2)$求三棱锥${A}{'}-BC'D$的体积.

$(1)$$\\dfrac{\\sqrt{3}}{3}$

$(2)$$\\dfrac{{a}^{3}}{3}$

$(1)$由图可知，

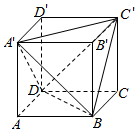
三棱锥${A}{'}-BC'D$是棱长为$\sqrt{2}a$的正四面体，
则其表面积为$4\times \dfrac{1}{2}×\sqrt{2}a×\sqrt{(\sqrt{2}a)^{2}-(\dfrac{\sqrt{2}}{2}a)^{2}}=2\sqrt{3}{a}^{2}$.
正方体的表面积为$6a^{2}$，
$\therefore $三棱锥${A}{'}-BC'D$的表面积与正方体的表面积的比值为$\dfrac{2\sqrt{3}{a}^{2}}{6{a}^{2}}=\dfrac{\sqrt{3}}{3}$；
$(2)$如图，三棱锥${A}{'}-BC'D$的体积为$V_{A’C}-4V_{{{A}{'}}-ABD}$，
$={a}^{3}-4×\dfrac{1}{3}×\dfrac{1}{2}×a×a×a=\dfrac{{a}^{3}}{3}$.