已知正四棱台$ABCD-A_1B_1C_1D_1$中，$AB=2A_1B_1=2$，$O$是底面$ABCD$的中心，若异面直线$OB_1$与$CC_1$所成角的余弦值为$\dfrac{7}{8}$，则该四棱台的侧面积为$(\qquad)$

$12$

$3\\sqrt{15}$

$6\\sqrt{3}$

$9$

如图所示，连接$AC$，$BD$，则$AC$∩$BD=O$，连接$A_1O$，$A_1C_1$，$B_1D_1$，
因为$AB=2A_1B_1=2$，所以$AC=2A_1C_1$，
则$OC=A_1C_1$，且$AC$∥$A_1C_1$，即$OC$∥$A_1C_1$，
所以四边形$A_1C_1CO$为平行四边形，则$A_1O$∥$CC_1$，且$A_1O=CC_1$，
所以∠$A_1OB_1$为异面直线$OB_1$与$CC_1$所成的角或其补角．，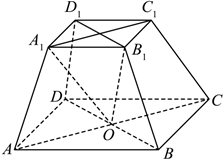
，
同理得四边形$B_1D_1DO$为平行四边形，则$B_1O=DD_1$，则$OB_1=OA_1$．，
因为直线$OB_1$与$CC_1$所成角的余弦值为$\dfrac{7}{8}$，
所以$\dfrac{{OA_1^2+OB_1^2-1}}{{2×O{A_1}×O{B_1}}}=\dfrac{7}{8}$，解得$OB_1=OA_1=2$，
在等腰梯形$ABB_1A_1$中，
由$AB=2A_1B_1=2$，$A_1A=B_1B=2$，则其高为$\sqrt{{2^2}-{{（{\dfrac{1}{2}}）}^2}}=\dfrac{{\sqrt{15}}}{2}$，
则侧面$ABB_1A_1$的面积为$\dfrac{1}{2}×（{2+1}）×\dfrac{{\sqrt{15}}}{2}=\dfrac{{3\sqrt{15}}}{4}$，
所以该四棱台的侧面积为$4×\dfrac{{3\sqrt{15}}}{4}=3\sqrt{15}$，
故选：$\rm B $．