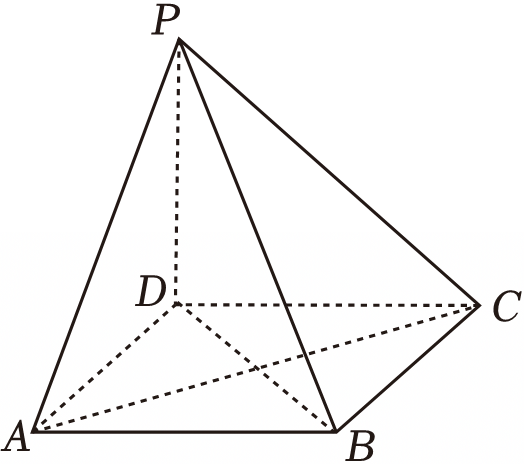
如图，在四棱锥$P-ABCD$中，$PD\perp$平面$ABCD$，底面$ABCD$是正方形，$AC$与$BD$交于点$O$．

$(1)$求证：$AC\perp$平面$PBD$．

$(2)$若$PD=AD=2$，求四棱锥$P-ABCD$的表面积．

$(1)$证明见解析；

$(2)$$8+4\\sqrt{2}$

$(1)$$\because $ 四边形$ABCD$是正方形，

$\therefore AC\perp BD$，

$\because PD\perp$平面$ABCD$，$AC\subset$平面$ABCD$，

$\therefore AC\perp PD$，又$BD\cap PD=D$，$BD$，$PD\subset$平面$PBD$，

$\therefore AC\perp$平面$PBD$；

$(2)$$\because PD\perp$平面$ABCD$，$AD$，$AB$，$BC$，$CD\subset$平面$ABCD$，

$\therefore PD\perp AD$，$PD\perp CD$，$PD\perp AB$，$PD\perp BC$，

$\because PD\perp AB$，$AB\perp AD$，$PD\cap AD=D$，$PD$，$AD\subset$平面$PAD$，

$\therefore AB\perp$平面$PAD$，又$PA\subset$平面$PAD$，

$\therefore AB\perp PA$，

$\because PD\perp BC$，$BC\perp CD$，$PD\cap CD=D$，$PD$，$CD\subset$平面$PCD$，

$\therefore BC\perp$平面$PCD$，又$PC\subset$平面$PCD$，

$\therefore BC\perp PC$，

$\because $ 四边形$ABCD$为正方形，$AD=2$，

$\therefore AB=BC=CD=2$，

又$PD=2$，$PD\perp AB$，$AB\perp AD$，

$\therefore PA=PC=2\sqrt{2}$，

$\therefore \triangle PAD$的面积${S}_{1}=\dfrac{1}{2}\times 2\times 2=2$，$\triangle PCD$的面积${S}_{2}=\dfrac{1}{2}\times 2\times 2=2$，

$\triangle PAB$的面积${S}_{3}=\dfrac{1}{2}\times 2\times 2\sqrt{2}=2\sqrt{2}$，$\triangle PCB$的面积${S}_{4}=\dfrac{1}{2}\times 2\times 2\sqrt{2}=2\sqrt{2}$，

又正方形$ABCD$的面积$S_{5}=4$，

$\therefore $ 四棱锥$P-ABCD$的表面积$S=8+4\sqrt{2}$．