| 8.6.2 直线与平面垂直 题目答案及解析
稿件来源:高途
| 8.6.2 直线与平面垂直题目答案及解析如下,仅供参考!
必修二
第八章 立体几何初步
8.6 空间直线、平面的垂直
8.6.2 直线与平面垂直
在正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中,$M$、$N$分别是$AB$、$AD$的中点,$E$、$F$、$P$分别是$B_{1}C_{1}$、$BB_{1}$、$DD_{1}$的中点.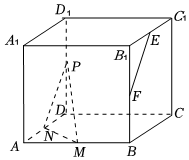 $(1)$证明:$MN//$平面$BDD_{1}B_{1}$;
$(1)$证明:$MN//$平面$BDD_{1}B_{1}$;
$(2)$证明:$CA_{1}\bot MN$;
$(3)$请判断直线$EF$与平面$MNP$位置关系(不需说明理由$)$.
$(1)$ 证明见解析
$(2)$ 证明见解析
$(3)$ $EF\\subset $平面$MNP$
$(1)$证明:$\because MN//BD$,$MN$⊄面$BDD_{1}B_{1}$,$BD\subset $平面$BDD_{1}B_{1}$,
$\therefore MN//$平面$BDD_{1}B_{1}$.
$(2)$证明:$AA_{1}\bot $平面$ABCD$,$MN\subset $平面$ABCD$,$\therefore AA_{1}\bot MN$,
$\because AC\bot BD,MN//BD$,$\therefore AC\bot MN$.
又$\because AA_{1}\cap AC=A$,$\therefore MN\bot $平面$A_{1}AC,\therefore CA_{1}\bot MN$.
$(3)$$EF\subset $平面$MNP($理由:取$C_1D_1$的中点$G$,连接$PG$,$EG$,$MF$,如图,可知$MNPGEF$是正六边形,所以$EF\subset $平面$MNP)$.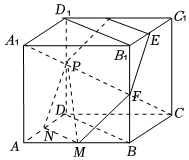 .
.
| 8.6.2 直线与平面垂直题目答案及解析(完整版)
