如图，在四棱锥$P-ABCD$中，底面$ABCD$为菱形，$\angle DAB=60^{\circ}$，侧面$PAD$为正三角形，且平面$PAD\bot $平面$ABCD$，则下列说法正确的是$ $ $(\qquad)$ $ $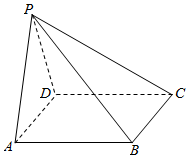

在棱$AD$上存在点$M$，使$AD\\bot $平面$PMB$

异面直线$AD$与$PB$所成的角为$90^{\\circ}$

二面角$P-BC-A$的大小为$45^{\\circ}$

$BD\\bot $平面$PAC$

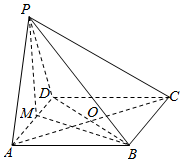如图所示，$\rm A$.取$AD$的中点$M$，连接$PM$，$BM$，连接对角线$AC$，$BD$相交于点$O$.
$\because $侧面$PAD$为正三角形，$\therefore PM\bot AD$.又底面$ABCD$为菱形，$\angle DAB=60^{\circ}$，$\therefore \triangle ABD$是等边三角形.
$\therefore AD\bot BM$.又$PM\cap BM=M.\therefore AD\bot $平面$PMB$，因此$\rm A$正确.
$\rm B$.由$\rm A$可得：$AD\bot $平面$PMB$，$\therefore AD\bot PB$，$\therefore $异面直线$AD$与$PB$所成的角为$90^{\circ}$，正确.
$\rm C$. $\because $平面$PBC\cap $平面$ABCD=BC,BC//AD$，$\therefore BC\bot $平面$PBM$，$\therefore BC\bot PB$，$BC\bot BM$.
$\therefore \angle PBM$是二面角$P-BC-A$的平面角，设$AB=1$，则$BM=\dfrac{\sqrt{3}}{2}=PM$，在$Rt\triangle PBM$中，$\tan \angle PBM=\dfrac{PM}{BM}=1,\therefore \angle PBM=45^{\circ}$，因此正确.
$\rm D$. $\because BD$与$PA$不垂直，$\therefore BD$与平面$PAC$不垂直，因此$\rm D$错误.
故选：$\rm ABC $.