如图，在长方形$ABCD$中，$AB=2$，$BC=1$，$E$为$DC$的中点，$F$为线段$EC($端点除外）上一动点，现将$\triangle AFD$沿$AF$折起，使平面$ABD\bot $平面$ABC$，在平面$ABD$内过点$D$作$DK\bot AB$，$K$为垂足，设$AK=t$，则$t$的取值范围是                  .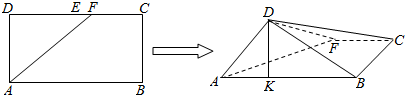

$(\\dfrac{1}{2}$，$1)$

此题的破解可采用二个极端位置法，即对于$F$位于$DC$的中点时，可得$t=1$，
随着$F$点到$C$点时，当$C$与$F$无限接近，不妨令二者重合，此时有$CD=2$，
因$CB\bot AB$，$CB\bot DK$，
$\therefore CB\bot $平面$ADB$，即有$CB\bot BD$，
对于$CD=2$，$BC=1$，在直角三角形$CBD$中，得$BD=\sqrt{3}$，
又$AD=1$，$AB=2$，再由勾股定理可得$\angle BDA$是直角，因此有$AD\bot BD$，
再由$DK\bot AB$，可得三角形$ADB$和三角形$AKD$相似，可得$t=\dfrac{1}{2}$，
因此$t$的取值的范围是$(\dfrac{1}{2}$，$1)$.