在四棱锥$P-ABCD$中，底面$ABCD$是边长为$2$的菱形，且$AB\bot $平面$PAD$，$BC\bot PC$.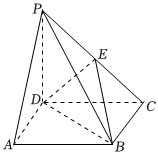
$(1)$证明：$BC\bot PD$；
$(2)$若$E$为$PC$的中点，异面直线$BE$与$PA$所成角的余弦值为$\dfrac{5\sqrt{2}}{8}$，$PA\geqslant 4$，求直线$PB$与平面$ABE$所成角的正弦值.

$(1)$ 证明见解析；
$(2)$ $\\dfrac{\\sqrt{105}}{35}$

$(1)$证明：因为$AB\bot $平面$PAD$，$AD$，$PD\subset $平面$PAD$，
所以$AB\bot AD$，$AB\bot PD$，
又因为底面$ABCD$是边长为$2$的菱形，所以可得四边形$ABCD$为正方形，
又因为$BC\bot PC$，$BC\bot CD$，$PC\cap CD=C$，
所以$BC\bot $平面$PCD$，$PD\subset $平面$PCD$，，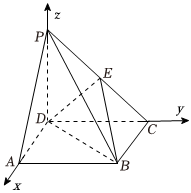
所以$BC\bot PD$；
$(2)$由$(1)$可得$BC\bot PD$，又因为$BC\cap AB=B$，
所以$PD\bot $底面$ABCD$，
以$D$为坐标原点，以$DA$，$DC$，$DP$所在的直线分别为$x$，$y$，$z$轴建立空间直角坐标系，
由题意可得$D\left(0,0,0\right),A\left(2,0,0\right)$，$C\left(0,2,0\right),B\left(2,2,0\right)$，
设$P\left(0,0,2c\right)$，$c \gt 0$，
则$PC$的中点$E\left(0,1,c\right),\overrightarrow{PA}=\left(-2,0,2c\right),\overrightarrow{BE}=\left(-2,-1,c\right)$，
因为$\overrightarrow{PA}\cdot \overrightarrow{BE}=4+2c^{2},|\overrightarrow{PA}|=\sqrt{4+4{c}^{2}},|\overrightarrow{BE}|=\sqrt{4+1+{c}^{2}}=\sqrt{5+{c}^{2}}$，
所以$\cos\lt \overrightarrow{PA},\overrightarrow{BE} \gt =\dfrac{\overrightarrow{PA}\cdot \overrightarrow{BE}}{|\overrightarrow{PA}|\cdot |\overrightarrow{BE}|}=\dfrac{4+2{c}^{2}}{\sqrt{4+4{c}^{2}}\cdot \sqrt{5+{c}^{2}}}$，
设异面直线$BE$与$PA$所成的角为$\theta $，$\theta \in \left[0,\dfrac{\pi }{2}\right]$，
所以$\cos \theta =|\cos\lt \overrightarrow{PA},\overrightarrow{BE} \gt |=\dfrac{4+2{c}^{2}}{\sqrt{4+4{c}^{2}}\cdot \sqrt{5+{c}^{2}}}=\dfrac{5\sqrt{2}}{8}$，
两边平方整理可得：$7c^{4}-22c^{2}+3=0$，
解得$c^{2}=\dfrac{1}{7}$或$c^{2}=3$，
因为$|PA|\geqslant 4$，所以$4+4c^{2}\geqslant 16$，可得$c^{2}\geqslant 3$，
所以$c^{2}=3$，即$c=\sqrt{3}$，
即$P(0,0,2\sqrt{3}$），$E(0,1,\sqrt{3})$，
此时$\overrightarrow{BP}=(-2,-2,2\sqrt{3}$），$\overrightarrow{AB}=\left(0,2,0\right),\overrightarrow{AE}=(-2,1,\sqrt{3})$，
设平面$ABE$的法向量为$\boldsymbol{n}=\left(x,y,z\right)$，
则$\left\{\begin{array}{l}{\boldsymbol{n}\cdot \overrightarrow{AB}=0}\\{\boldsymbol{n}\cdot \overrightarrow{AE}=0}\end{array}\right.$，即$\left\{\begin{array}{l}{2y=0}\\{-2x+y+\sqrt{3}z=0}\end{array}\right.$，
令$z=2$，
可得$\boldsymbol{n}=\left(\sqrt{3},0,2\right)$，
所以$\boldsymbol{n}\cdot \overrightarrow{BP}=-2\sqrt{3}+0+4\sqrt{3}=2\sqrt{3},|\boldsymbol{n}|=\sqrt{3+0+4}=\sqrt{7},|\overrightarrow{BP}|=\sqrt{4+4+12}=2\sqrt{5}$，
所以$\cos\lt \boldsymbol{n},\overrightarrow{BP} \gt =\dfrac{\boldsymbol{n}\cdot \overrightarrow{BP}}{|\boldsymbol{n}|\cdot |\overrightarrow{BP}|}=\dfrac{2\sqrt{3}}{\sqrt{7}×2\sqrt{5}}=\dfrac{\sqrt{105}}{35}$.
设直线$PB$与平面$ABE$所成的角为$\varphi $，$\varphi \in \left[0,\dfrac{\pi }{2}\right]$，
所以$\sin \varphi =|\cos\lt \boldsymbol{n},\overrightarrow{BP} \gt |=\dfrac{\sqrt{105}}{35}$.
即直线$PB$与平面$ABE$所成角的正弦值为$\dfrac{\sqrt{105}}{35}$.