以棱长为$1$的正方体各面的中心为顶点，构成一个正八面体，那么这个正八面体的表面积是                 ．

根据题意，以棱长为$1$的正方体各面的中心为顶点，构成一个正八面体，设所得正八面体的棱长为$a$，

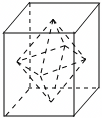
则这个正八面体的中截面（垂直平分相对顶点连线的界面）是正方形，

且正方形对角线长等于正方体的棱长$1$，则$\sqrt{2}a=1$，解可得$a=\dfrac{\sqrt{2}}{2}$，

又由该正八面体的每个面都是等边三角形，

则其表面积$S=8\times \left(\dfrac{1}{2}\times \dfrac{\sqrt{2}}{2}\times \dfrac{\sqrt{2}}{2}\times \dfrac{\sqrt{3}}{2}\right)=\sqrt{3}$．

故答案为：$\sqrt{3}$