把一个三边均为有理数的直角三角形面积的数值称为同余数，如果正整数$n$为同余数，则称$n$为整同余数．在$\triangle ABC$中，$C=\dfrac{\pi }{2}$，$\triangle ABC$绕$AC$旋转一周，所成几何体的侧面积和体积的数值之比为$\dfrac{5}{4}$，若$\triangle ABC$的面积$n$为整同余数，则$n$的值可以为$(\qquad)$．

$5$

$6$

$8$

$12$

根据题意，在$\triangle ABC$中，$C=\dfrac{\pi }{2}$，将$\triangle ABC$绕$AC$旋转一周，所成的几何体为圆锥，如图：

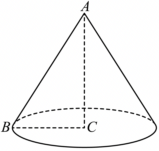
则该圆锥的侧面积为$S=\pi \times BC\times AB$，其体积为$V=\dfrac{1}{3}\pi \times B{C}^{2}\times AC$，

若$\dfrac{S}{V}=\dfrac{\pi \times BC\times AB}{\dfrac{1}{3}\pi \times B{C}^{2}\times AC}=\dfrac{3AB}{BC\times AC}=\dfrac{5}{4}$，变形可得$12AB=5BC\times AC$，

由此依次分析选项：

对于$\rm A$，若$n=5$，此时${S}_{\triangle ABC}=\dfrac{1}{2}BC\times AC=5$，变形可得$BC\times AC=10$，

又由$12AB=5BC\times AC=50$，可得$AB=\dfrac{50}{12}=\dfrac{25}{6}$，

则有$\begin{cases}BC\times AC=10\\ AB=\sqrt{B{C}^{2}+A{C}^{2}}=\dfrac{25}{6}\end{cases}$，变形可得$B{C}^{4}-\dfrac{625}{36}B{C}^{2}+100=0$，

$\because $ $\varDelta=\left( \dfrac{625}{36}\right)^{2}-400=\dfrac{-127775}{36\times36}\lt0$，

$\therefore $ 方程$B{C}^{4}-\dfrac{625}{36}B{C}^{2}+100=0$无解，不符合题意，$\rm A$错误；

对于$\rm B$，若$n=6$，此时${S}_{\triangle ABC}=\dfrac{1}{2}BC\times AC=6$，变形可得$BC\times AC=12$，即$12AB=5BC\times AC=60$，可得$AB=5$，

则有$\begin{cases}BC\times AC=12\\ AB=\sqrt{B{C}^{2}+A{C}^{2}}=5\end{cases}$，解可得$\begin{cases}BC=3\\ AC=4\end{cases}$或$\begin{cases}BC=4\\ AC=3\end{cases}$，

此时$\triangle ABC$的三边都是有理数，符合题意，$\rm B$正确；

对于$\rm C$，若$n=8$，则${S}_{\triangle ABC}=\dfrac{1}{2}BC\times AC=8$，可得$BC\times AC=16$，$12AB=5BC\times AC=80$，

可得$AB=\dfrac{80}{12}=\dfrac{20}{3}$，

则有$\begin{cases}BC\times AC=16\\ AB=\sqrt{B{C}^{2}+A{C}^{2}}=\dfrac{20}{3}\end{cases}$，变形可得${(BC+AC)}^{2}-2BC\times AC=\dfrac{400}{9}$，

则有$BC+AC=\dfrac{4\sqrt{43}}{3}$，

解得$\begin{cases}BC=\dfrac{2\sqrt{43}}{3}-\dfrac{2\sqrt{7}}{3}\\ AC=\dfrac{2\sqrt{43}}{3}+\dfrac{2\sqrt{7}}{3}\end{cases}$或$\begin{cases}BC=\dfrac{2\sqrt{43}}{3}+\dfrac{2\sqrt{7}}{3}\\ AC=\dfrac{2\sqrt{43}}{3}-\dfrac{2\sqrt{7}}{3}\end{cases}$，

此时$BC$，$AC$是无理数，不符合题意，$\rm C$错误；

对于$\rm D$，若$n=12$，则${S}_{\triangle ABC}=\dfrac{1}{2}BC\times AC=12$，可得$BC\times AC=24$，

又由$12AB=5BC\times AC=120$，可得$AB=10$，

由$\begin{cases}BC\times AC=24\\ AB=\sqrt{B{C}^{2}+A{C}^{2}}=10\end{cases}$，变形可得$(BC+AC)^{2}-2BC\times AC=100$，

$\therefore (BC+AC)^{2}=148$，即$BC+AC=2\sqrt{37}$，

解得$\begin{cases}BC=\sqrt{37}-\sqrt{13}\\ AC=\sqrt{37}+\sqrt{13}\end{cases}$或$\begin{cases}BC=\sqrt{37}+\sqrt{13}\\ AC=\sqrt{37}-\sqrt{13}\end{cases}$，

此时$BC$，$AC$都是无理数，不符合题意，$\rm D$错误．

故选：$\rm B$