已知圆台上、下底面的圆周都在一个直径为$10$的球面上，其上、下底面半径分别为$4$和$5$，则该圆台的侧面积                 ．

$9\\sqrt{10}\\pi $．

解：圆台的下底面半径为$5$，故下底面在外接球的大圆上，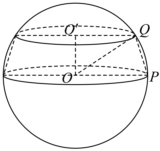
如图所示，设球的球心为$O$，圆台上底面的圆心为$O$′，
则圆台的高$OO′=\sqrt{O{Q}^{2}-O′{Q}^{2}}=\sqrt{{5}^{2}-{4}^{2}}=3$，
测圆台的母线长为$\sqrt{{3}^{2}+{(5-4)}^{2}}=\sqrt{10}$，
据此可得圆台的侧面积为$\pi ×\sqrt{10}×(4+5)=9\sqrt{10}\pi $．
故答案为：$9\sqrt{10}\pi $．