攒尖是我国古代建筑中屋顶的一种结构形式，通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖，多见于亭阁式建筑、园林建筑．下面以四角攒尖为例，如图，它的屋顶部分的轮廓可近似看作一个正四棱锥，已知此正四棱锥的侧面与底面所成的二面角为$30{}^\circ $，侧棱长为$\sqrt{21}$米，则该正四棱锥的$(\qquad)$．

底面边长为$6$米

侧棱与底面所成角的正弦值为$\\dfrac{\\sqrt{7}}{7}$

侧面积为$24\\sqrt{3}$平方米

体积为$12\\sqrt{3}$立方米

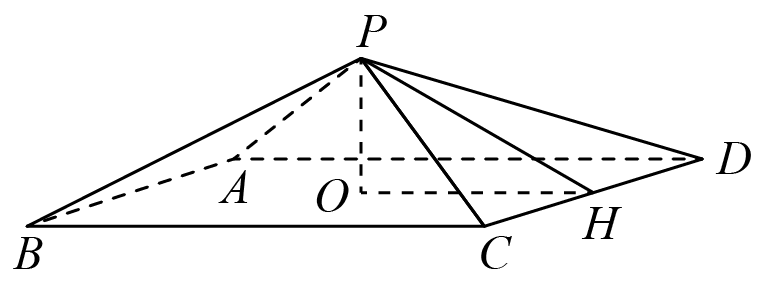
如图，在正四棱锥${{P}-{ABCD}}$中，设底面边长为$2a$．

设$O$为正方形$ABCD$的中心，$H$为$CD$的中点，

则$PH\perp CD$，$OH\perp CD$，

$∴$  $\angle PHO$为二面角$P-CD-O$的平面角，

又正四棱锥的侧面与底面所成的二面角为$30{}^\circ $，

$\because \angle PHO=30{}^\circ $，

$∴$  $OH=DH=a,OP=\dfrac{\sqrt{3}}{3}a,PH=\dfrac{2\sqrt{3}}{3}a$．

在$\triangle PCH$中，${{a}^{2}}+{{\left( \dfrac{2\sqrt{3}}{3}a \right)}^{2}}=21$，

$\therefore a=3$，即底面边长为$6$米，故$\rm A$正确，

$∴$  $PO=\sqrt{3}$，$PH=2\sqrt{3}$，$PC=\sqrt{21}$,

又侧棱$PC$与底面所成的角为$\angle PCO$，$\sin \angle PCO=\dfrac{PO}{PC}=\dfrac{\sqrt{3}}{\sqrt{21}}=\dfrac{\sqrt{7}}{7}$,故$\rm B$正确，

正四棱锥的侧面积$S=\dfrac{1}{2}\times 6\times 2\sqrt{3}\times 4=24\sqrt{3}$平方米．故$\rm C$正确，

正四棱锥的体积$V=\dfrac{1}{3}\times 36\times \sqrt{3}=12\sqrt{3}$，故$\rm D$正确，

故选：$\rm ABCD$$.$