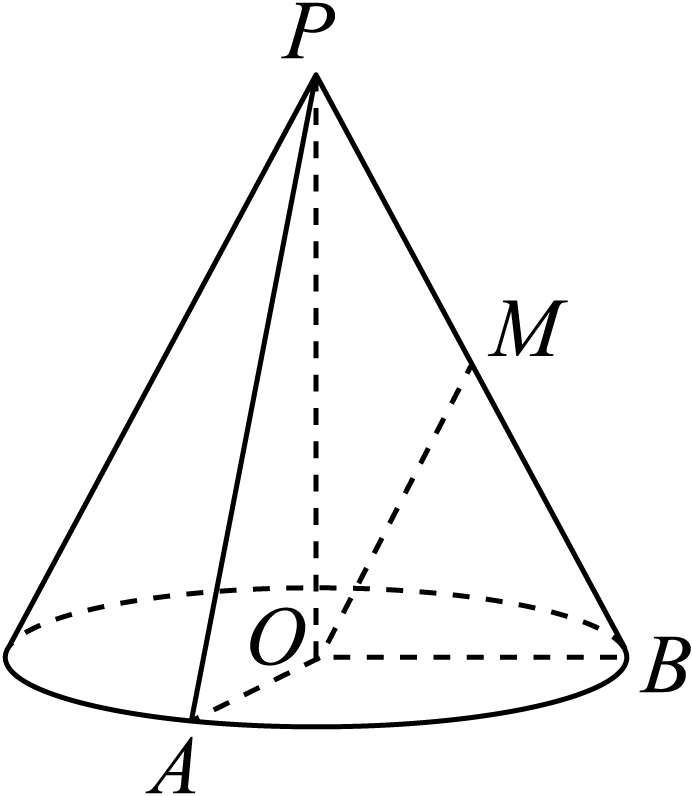
如图，圆锥的顶点为$P$，底面半径$OA$与$OB$相互垂直，点$M$是母线$PB$的中点，已知$OA=OM=2$．

$(1)$求该圆锥的表面积；

$(2)$求异面直线$OM$与$AP$所成角的大小．

$(1)$$12\\pi$；

$(2)$$\\arccos \\dfrac{3}{4}$．

$(1)$由已知得：$PO\perp OB$，又直线$PB$的中点为$M$，

$\therefore PB=2OM=4$，

$\therefore $母线$l=4$，

底面半径为$r=OA=2$，

$\therefore {{S}_{}}=\pi lr+\pi {{r}^{2}}=\pi \times 4\times 2+\pi \times {{2}^{2}}=12\pi $

$(2)$如图，

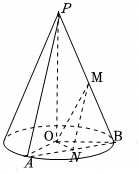
$\because OB=2$，$PA=PB=4$，连接$AB$且取$AB$的中点$N$，

又$PB$的中点为$M$，连接$MN$，则$MN//AP$，且$MN=2$，

$\therefore \angle OMN$就是异面直线$AP$与$OM$所成的角（或其补角），

易知$OM=\dfrac{1}{2}PB=2$，

在$Rt$$\triangle $$OAN$中，$\angle AON=60^\circ$，

$\therefore ON=OA\cos 60^\circ =1$，

在$\triangle $$OMN$中，$\cos \angle OMN=\dfrac{O{M}^{2}+M{N}^{2}-O{N}^{2}}{2OM\cdot MN}=\dfrac{3}{4}$，

即异面直线$OM$与$AP$所成角的大小为$\arccos \dfrac{3}{4}$．