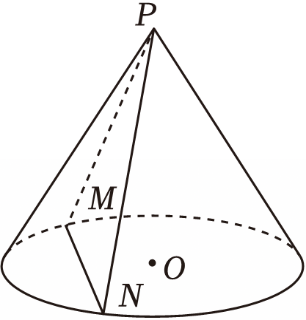
如图，圆锥$OP$的高$h=1$，侧面积$S=2\sqrt{3}\pi$，$M$，$N$是底面圆$O$上的两个动点，则$\triangle $$PMN$面积的最大值为$(\qquad)$．

$\\sqrt{3}$

$2$

$1$

$\\dfrac{1}{2}$

设圆锥$OP$的母线为$l$，

$\because $ 圆锥$OP$的高$h=1$，侧面积$S=2\sqrt{3}\pi$，

由$S=\pi rl=2\sqrt{3}\pi$，得$rl=2\sqrt{3}$，①

由$l^{2}=r^{2}+h^{2}=r^{2}+1$，②，

联立①②解得$r=\sqrt{3}$，$l=2$，

则圆锥$OP$轴截面的顶角为$\dfrac{2\pi }{3}$，

$\therefore $ $\triangle $$PMN$的面积为$\dfrac{1}{2}PM\cdot PN\sin \angle MPN\le \dfrac{1}{2}PM\cdot PN=2$．

故选：$\rm B$