| 洛伦兹力 题目答案及解析
稿件来源:高途
| 洛伦兹力题目答案及解析如下,仅供参考!
选修3-1
第三章 磁场
3.5 运动电荷在磁场中受到的力
洛伦兹力
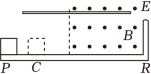
如图所示,$PR$是一块长为$L=4\ \rm m$的绝缘平板固定在水平地面上,整个空间有一个平行于$PR$的匀强电场$E$,在板的右边一半的部分有一个垂直于纸面向外的匀强磁场$B$,一个质量为$m=0.1\;\rm kg$,带电量为$q=0.5\;\rm C$的物体,从板的$P$端由静止开始在电场力和摩擦力的作用下向右做匀加速运动,进入磁场后恰能做匀速运动。当物体碰到板$R$端的挡板后被弹回,若在碰撞瞬间撤去电场,物体返回时在磁场中仍做匀速运动,离开磁场后做匀减速运动停在$C$点,$PC=\dfrac{L}{4}$,物体与平板间的动摩擦因数为$\mu =0.4$,取$g=10\;\rm m/{{s}^{2}}$,求:
分析判断物体带电性质,正电荷还是负电荷?
物体带正电;
"]]由题意知,物体返回时在磁场中仍做匀速运动,洛伦兹力方向向上,则知物体带正电;
物体与挡板碰撞后的速度${{v}_{2}}$;
物体与挡板碰撞后的速度为$2\\sqrt{2}\\;\\rm m/s$,方向向左;
"]]物体返回后在磁场中无电场,仍做匀速运动,洛伦兹力与重力平衡,则有$mg=qB{{v}_{2}}$
离开磁场后,由动能定理得$-\mu mg\cdot \dfrac{L}{4}=0-\dfrac{1}{2}mv_{2}^{2}$
解得${{v}_{2}}=2\sqrt{2}\;\rm m/s$,方向向左,$B=\dfrac{\sqrt{2}}{2}T$;
磁感应强度$B$的大小;
磁感应强度$B$的大小为$\\dfrac{\\sqrt{2}}{2}\\ \\rm T$;
"]]物体返回后在磁场中无电场,仍做匀速运动,洛伦兹力与重力平衡,则有$mg=qB{{v}_{2}}$
离开磁场后,由动能定理得$-\mu mg\cdot \dfrac{L}{4}=0-\dfrac{1}{2}mv_{2}^{2}$
解得${{v}_{2}}=2\sqrt{2}\;\rm m/s$,方向向左,$B=\dfrac{\sqrt{2}}{2}\ \rm T$;
电场强度$E$的大小和方向。
电场强度$E$的大小为$2.4\\;\\rm N/C$,方向水平向右。
"]]由于物体由$P$运动到$C$做匀加速运动,可知电场方向水平向右,且有$(Eq-\mu mg)\dfrac{L}{2}=\dfrac{1}{2}mv_{1}^{2}$
进入电磁场后做匀速运动,则有$qE=\mu (qB{{v}_{1}}+mg)$
解得$E=2.4\;\rm N/C$。
| 洛伦兹力题目答案及解析(完整版)
