质谱仪的工作原理如图所示，大量粒子飘入加速电场，其初速度几乎为$0$，经过加速后，通过宽为$L$的狭缝$MN$沿着与磁场垂直的方向进入匀强磁场中，最后打到照相底片上。在一次测试中，大量的某种粒子经加速电场加速后刚进入匀强磁场时的速度大小均为$v$，打在底片上的位置到$M$点的最小距离为$a$，匀强磁场的磁感应强度为$B$，不考虑粒子的重力及它们之间的相互作用。则$(\qquad)$

粒子的比荷为$\\dfrac{2v}{B(a+L)}$

加速电场的电压为$\\dfrac{B(a+L)v^{2}}{4}$

粒子在磁场中运动的时间$\\dfrac{\\pi(a+L)}{v}$

大量粒子所经过磁场区域最窄外的宽度为$\\dfrac{a+L-\\sqrt{a^{2}+2aL}}{2}$

$\rm A$．粒子在磁场中做匀速圆周运动，轨道半径为$r=\dfrac{a+L}{2}$

根据牛顿第二定律可得$qvB=m\dfrac{v^{2}}{r}$

解得$\dfrac{q}{m}=\dfrac{2v}{B(a+L)}$

故$\rm A$正确；

$\rm B$．粒子在电场中加速，根据动能定理可得$qU=\dfrac{1}{2}mv^{2}$

联立，可得$U=\dfrac{B(a+L)v}{4}$

故$\rm B$错误；

$\rm C$．粒子在磁场中做匀速圆周运动的周期为$T=\dfrac{2\pi r}{v}$

粒子在磁场中运动的时间为$t=\dfrac{T}{2}$

联立可得$t=\dfrac{\pi(a+L)}{2v}$

故$\rm C$错误；

$\rm D$．粒子在磁场中经过的区域为图中的阴影部分，

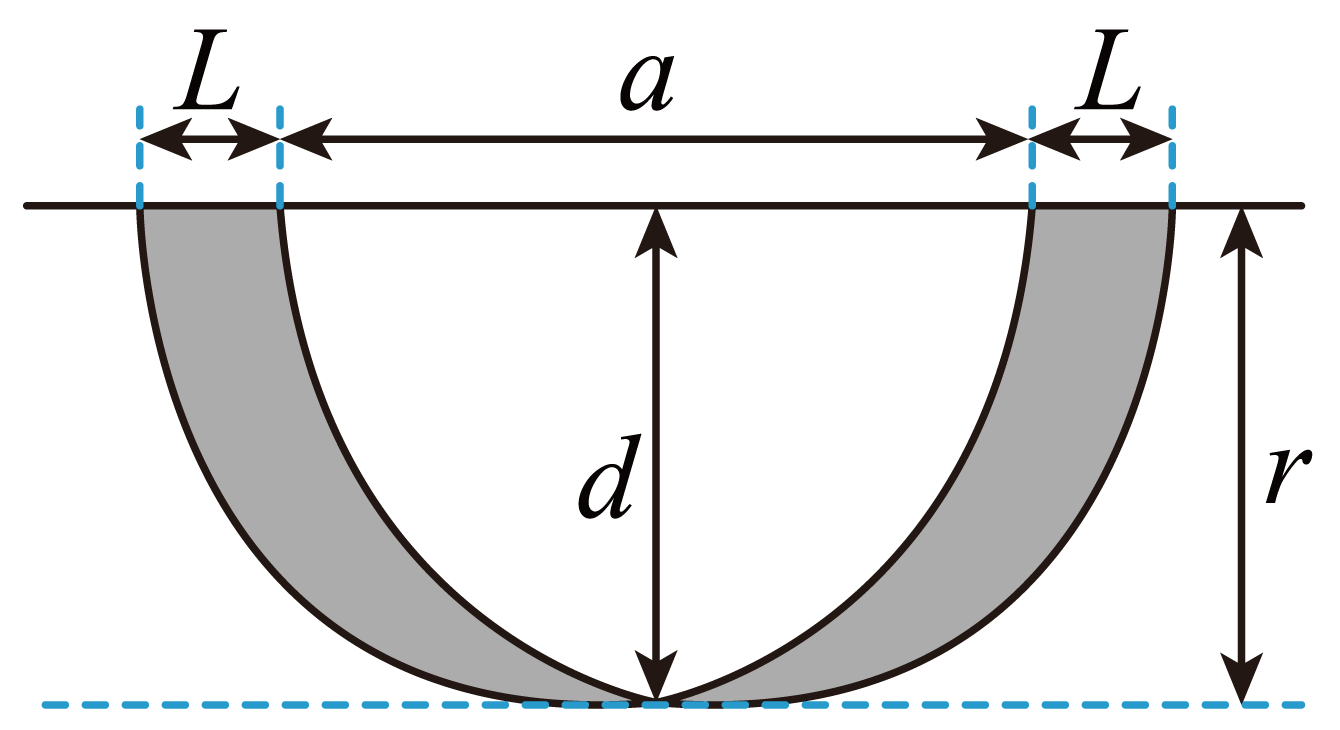
根据几何关系有$d=\sqrt{r^{2}-\left( \dfrac{2L-a}{2}-r \right)^{2}}$

最窄处的宽度为$\Delta d=r − d$

联立，可得$\Delta d=\dfrac{a+L-\sqrt{a^{2}+2aL}}{2}$

故$\rm D$正确。

故选：$\rm AD$。