高中 | 速度选择器 题目答案及解析
稿件来源:高途
高中 | 速度选择器题目答案及解析如下,仅供参考!
选修3-1
第三章 磁场
3.6 带电粒子在匀强磁场中的运动
速度选择器
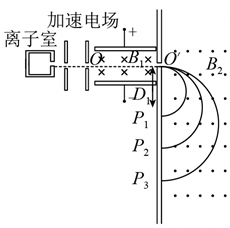
质谱仪是由离子室、加速电场、速度选择器和分离器四部分组成的。已知速度选择器的两极板间的匀强电场的电场强度大小为$E$,匀强磁场的磁感应强度大小为$B_{1}$、方向垂直纸面向里,分离器中匀强磁场的磁感应强度大小为$B_{2}$,方向垂直纸面向外。离子室内充有大量氢的同位素氕$\rm _{1}^{1}H$、氘$\rm _{1}^{2}H$、氚$\rm _{1}^{3}H$,它们以不同的速度经加速电场加速后,从速度选择器两极板间的中点$O$平行于极板进入,部分粒子沿直线通过小孔$O'$后进入分离器的偏转磁场中,最后在底片上形成了对应于氕$\rm _{1}^{1}H$、氘$\rm _{1}^{2}H$、氚$\rm _{1}^{3}H$三种离子的三个感光点$P_{1}$、$P_{2}$、$P_{3}$,测得$P_{1}$到$O'$点的距离为$d$。不计离子所受的重力及它们之间的相互作用。求:
打在$P_{1}$处的离子的比荷$\dfrac{q}{m}$;
打在$P_{1}$处的离子的比荷$\\dfrac{q}{m}$为$\\dfrac{2E}{B_{1}B_{2}d}$
"]]离子通过速度选择器时,做匀速直线运动,则有$qvB_{1}=qE$
解得$v= \dfrac{E}{B_{1}}$
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得$qvB_{2}=m\dfrac{v^{2}}{r}$
其中$r= \dfrac{d}{2}$
联立可得$\dfrac{q}{m}=\dfrac{2E}{B_{1}B_{2}d}$
$P_{2}$与$P_{3}$两点间的距离$d'$。
$P_{2}$与$P_{3}$两点间的距离$d'$为$d$
"]]氘离子打在$P_{2}$的位置,令$O'P_{2}$的距离为$x_{2}$,粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得$qvB_{2}=2m\dfrac{v^{2}}{\dfrac{x_{2}}{2}}$
氚打在$P_{3}$的位置,令$O'P_{3}$的距离为$x_{3}$,粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得$qvB_{2}=3\dfrac{v^{2}}{\dfrac{x_{3}}{2}}$
$P_{2}$与$P_{3}$两点间的距离为$d'=P_{3}-P_{2}$
联立可得$d'= \dfrac{B_{1}vd}{E} =d$
高中 | 速度选择器题目答案及解析(完整版)
