如图，带等量正电荷$q$的$M$、$N$两种粒子，以几乎为$0$的初速度从$S$飘入电势差为$U$的加速电场，经加速后从$O$点沿水平方向进入速度选择器（简称选择器）。选择器中有竖直向上的匀强电场和垂直纸面向外的匀强磁场。当选择器的电场强度大小为$E$，磁感应强度大小为$B_{1}$，右端开口宽度为$2d$时，$M$粒子沿轴线$OO^\prime$穿过选择器后，沿水平方向进入磁感应强度大小为$B_{2}$、方向垂直纸面向外的匀强磁场（偏转磁场），并最终打在探测器上；$N$粒子以与水平方向夹角为$\theta$的速度从开口的下边缘进入偏转磁场，并与$M$粒子打在同一位置，忽略粒子重力和粒子间的相互作用及边界效应，则$(\qquad)$

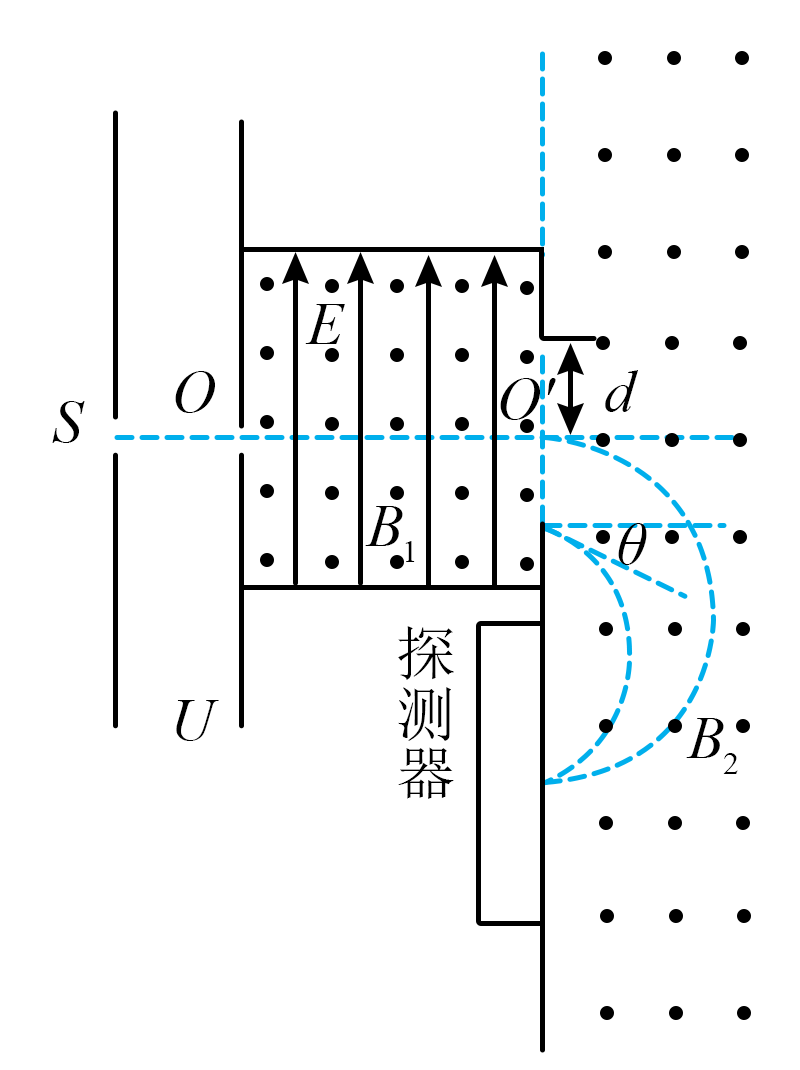
$M$粒子质量为$\\dfrac{2qUB_{1}^{2}}{E^{2}}$

刚进入选择器时，$N$粒子的速度小于$M$粒子的速度

调节选择器，使$N$粒子沿轴线$OO^\\prime$穿过选择器，此时选择器的电场强度与磁感应强度大小之比为$\\dfrac{4EU\\cos\\theta}{4UB_{1}-EdB_{2}}$

调节选择器，使$N$粒子沿轴线$OO^\\prime$进入偏转磁场，打在探测器上的位置与调节前$M$粒子打在探测器上的位置间距为$\\dfrac{4UB_{1}}{EB_{2}}+\\dfrac{\\left( EdB_{2}-4UB_{1} \\right)\\sqrt{U}}{EB_{2}\\sqrt{U-Ed}\\cos\\theta}$

$\rm A$．对$M$粒子在加速电场中$qU=\dfrac{1}{2}m_{M}v_{0M}^{2}$

在速度选择器中$qv_{0M}B_{1}=qE$

解得$M$的质量$m_{M}=\dfrac{2qUB_{1}^{2}}{E^{2}}$，故$\rm A$正确；

$\rm B$．进入粒子速度选择器后因$N$粒子向下偏转，可知$qv_{0N}B_{1}\gt qE$

即$v_{0N}\gt v_{0M}$，故$\rm B$错误；

$\rm C$．$M$粒子在磁场中运动半径为$r_{1}$，则$qv_{0M}B_{2}=m_{M}\dfrac{v_{0M}^{2}}{r_{1}}$

解得$r_{1}=\dfrac{m_{M}v_{0M}}{qB_{2}}=\dfrac{2UB_{1}}{EB_{2}}$

$N$粒子在磁场中运动的半径为$r_{2}$，则$2r_{1}-2r_{2}\cos \theta=d$

解得$r_{2}=\dfrac{4UB_{1}-EB_{2}d}{2EB_{2}\cos\theta}$

其中$qv_{N}B_{2}=m_{N}\dfrac{v_{N}^{2}}{r_{2}}$

可得$v_{N}=\dfrac{4UqB_{1}-EB_{2}qd}{2Em_{N}\cos\theta}$

由动能定理$N$粒子在选择器中$- Edq=\dfrac{1}{2}m_{N}v_{N}^{2}-\dfrac{1}{2}m_{N}v_{0N}^{2}$

在加速电场中$Uq=\dfrac{1}{2}m_{N}v_{0N}^{2}$

解得$m_{N}=\dfrac{q{(4UB_{1}-EB_{2}d)}^{2}}{8E^{2}\cos^{2}\theta(U-Ed)}$，$v_{0N}=\dfrac{4E\cos\theta\sqrt{U(U-Ed)}}{4UB_{1}-EB_{2}d}$

则要想使得粒子$N$沿轴线$OO'$通过选择器，则需满足$qv_{0N}B_{1}'=qE'$

联立解得$\dfrac{E'}{B'_{1}}=v_{0N}=\dfrac{4E\cos\theta\sqrt{U(U-Ed)}}{4UB_{1}-EB_{2}d}$，故$\rm C$错误；

$\rm D$．若$N$粒子沿直线通过选择器，则在磁场中运动的半径为$r_{3}$，则打在探测器的位移与调节前$M$打在探测器上的位置间距为$\Delta x=2r_{3} − 2r_{1}$

其中$r_{1}=\dfrac{m_{M}v_{0M}}{qB_{2}}=\dfrac{2UB_{1}}{EB_{2}}$，$r_{3}=\dfrac{m_{N}v_{0N}}{qB_{2}}=\dfrac{(4UB_{1}-EB_{2}d)\sqrt{U}}{2B_{2}E\cos\theta\sqrt{U-Ed}}$

可得$\Delta x=\dfrac{(4UB_{1}-EB_{2}d)\sqrt{U}}{B_{2}E\cos\theta\sqrt{U-Ed}}+\dfrac{4UB_{1}}{EB_{2}}$，故$\rm D$正确。

故选：$\rm AD$。