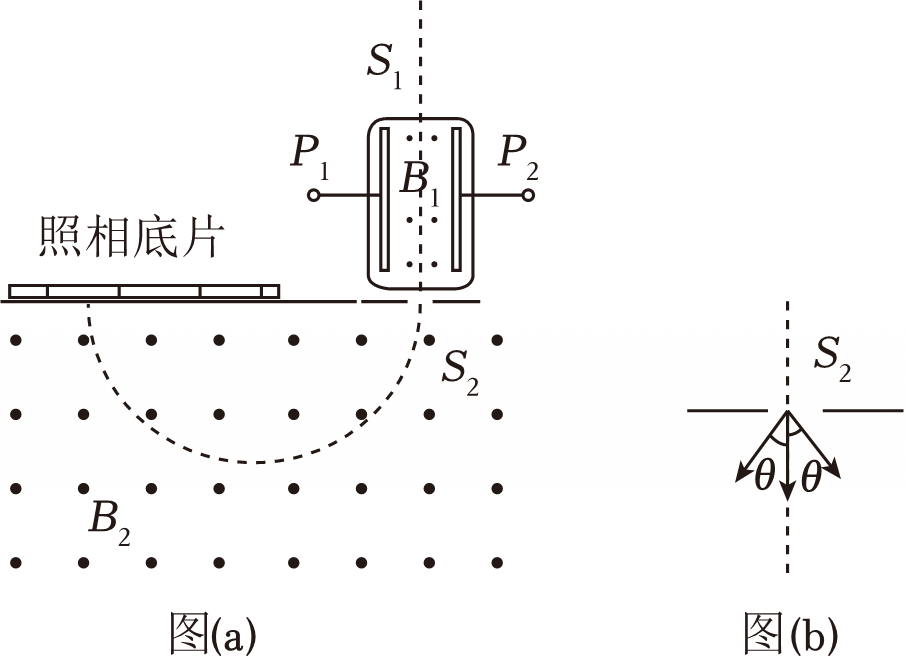
氢离子$(\rm _{1}^{1}H)$进入$B_{2}$区域的速度$v_{0}$大小；

氢离子$(\\rm _{1}^{1}H)$进入$B_{2}$区域的速度$v_{0}$大小为$\\dfrac{U}{B_{1}d}$

带电粒子在$P_{1}$和$P_{2}$两金属板间运动时，电场与洛伦兹力平衡$qv_{0}B_{1}=q\dfrac{U}{d}$

解得$v_{0}=\dfrac{U}{B_{1}d}$

若有两种粒子沿中心线从$S_{2}$进入$B_{2}$区域，打到底片的位置距$S_{2}$的距离分别为$x_{1}$和$x_{2}$，求两种粒子的比荷之比；

若有两种粒子沿中心线从$S_{2}$进入$B_{2}$区域，打到底片的位置距$S_{2}$的距离分别为$x_{1}$和$x_{2}$，两种粒子的比荷之比为$\\dfrac{x_{2}}{x_{1}}$

两种粒子进入磁场时的速度相同，根据$qv_{0}B_{2}=m\dfrac{v_{0}^{2}}{r}$

可得$r=\dfrac{mv_{0}}{qB_{2}}$

打到底片的位置距$S_{2}$的距离$x=2r=\dfrac{2mv_{0}}{qB_{2}}$

可得$\dfrac{q}{m}=\dfrac{2U}{B_{1}B_{2}dx} \propto \dfrac{1}{x}$

两种粒子的比荷之比$\dfrac{x_{2}}{x_{1}}$

受到其他因素影响，发现从$S_{2}$射入的氢离子$(\rm _{1}^{1}H)$速度方向有微小的发散角$\theta$，如图（$\rm b$）所示，使得氢离子打在照相底片上会形成一条亮线，测得最大的发散角的余弦值$\cos\theta=0.9$，求该亮线的长度$L$；

长度$L$为$\\dfrac{mU}{5qB_{1}B_{2}d}$

在磁场中粒子运动的半径为$r=\dfrac{mv_{0}}{qB_{2}}$

离子运动的轨道边界线如图所示

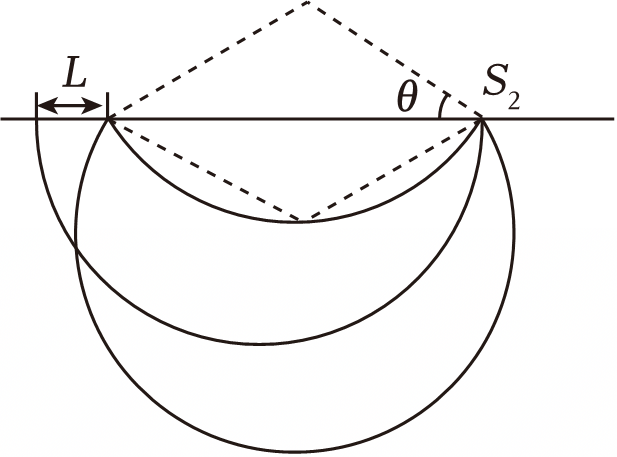
亮线长度为$L=2r-2r\cos\theta=\dfrac{mU}{5qB_{1}B_{2}d}$

在分离氢元素的三种同位素离子($\rm _{1}^{1}H$、$\rm _{1}^{2}H$、$\rm _{1}^{3}H$)时，各种离子有微小的发散角$\theta(\cos\theta=0.9)$外，其速度还有波动，即$v_{0}-\Delta v\leqslant v\leqslant v_{0}+\Delta v$，要能有效区分出同位素离子，照相底片上亮线之间的间距应不小于相邻较短亮线长度的十分之一，则$\dfrac{\Delta v}{v_{0}}$应满足什么条件？（保留两位小数）

在分离氢元素的三种同位素离子($\\rm _{1}^{1}H$、$\\rm _{1}^{2}H$、$\\rm _{1}^{3}H$)时，各种离子有微小的发散角$\\theta(\\cos\\theta=0.9)$外，其速度还有波动，即$v_{0}-\\Delta v\\leqslant v\\leqslant v_{0}+\\Delta v$，要能有效区分出同位素离子，照相底片上亮线之间的间距应不小于相邻较短亮线长度的十分之一，则$\\dfrac{\\Delta v}{v_{0}}$应满足$\\dfrac{\\Delta v}{v_{0}} \\leqslant 0.44$

各离子运动的最大和最小半径分别为$r_{\max}=\dfrac{m(v_{0}+\Delta v)}{eB_{2}}$，$r_{\min}=\dfrac{m(v_{0}-\Delta v)}{eB_{2}}$

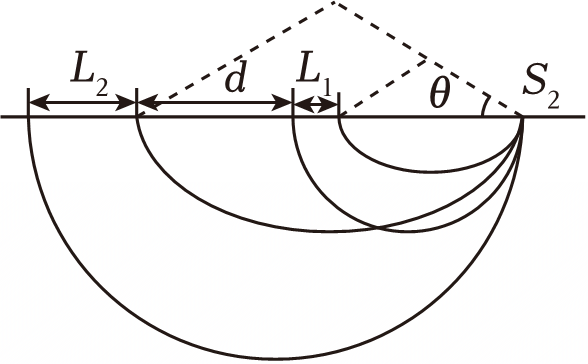
各离子最远位置到$S_{2}$的距离为$2r_{\max}$，最近位置到$S_{2}$的距离为$2r_{\min}\cos\theta$，通过作图可知，要求两条亮线间距不小于相邻较短亮线长度的十分之一，即$\dfrac{2m_{2}(v_{0}-\Delta v)}{eB_{2}}\cos\theta-\dfrac{2m_{1}v_{0}}{eB_{2}} \geqslant \dfrac{1}{10} \times \dfrac{2m_{1}v_{0}}{eB_{2}}(1-\cos\theta)$

其中$m_{2}=2m_{1}$，$\cos\theta=0.9$

解得$\dfrac{\Delta v}{v_{0}} \leqslant 0.44$