下图为无线充电技术中使用的受电线圈示意图，线圈匝数为$n$，面积为$S$。若在$t_{1}$到$t_{2}$时间内，匀强磁场平行于线圈轴线向右穿过线圈，其磁感应强度大小由$B_{1}$均匀增加到$B_{2}$，则该段时间线圈两端$a$和$b$之间的电势差$U_{ab}(\qquad)$

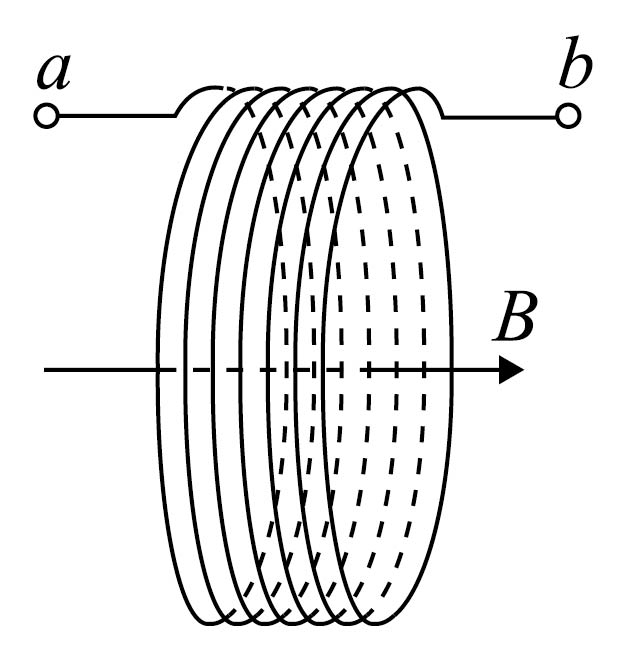
恒为$\\dfrac{nS\\left( B_{2}-B_{1} \\right)}{t_{2}-t_{1}}$

从$0$均匀变化到$\\dfrac{nS\\left( B_{2}-B_{1} \\right)}{t_{2}-t_{1}}$

恒为$- \\dfrac{nS\\left( B_{2}-B_{1} \\right)}{t_{2}-t_{1}}$

从$0$均匀变化到$- \\dfrac{nS\\left( B_{2}-B_{1} \\right)}{t_{2}-t_{1}}$

恒为$0$

穿过线圈的磁场均匀增加，将产生大小恒定的感生电动势，由法拉第电磁感应定律得$E=n\dfrac{\Delta\Phi}{\Delta t}=n\dfrac{S\left( B_{2}-B_{1} \right)}{t_{2}- t_{1}}$，而等效电源内部的电流由楞次定理知从$a→b$，即$b$点是等效电源的正极，即$U_{ab}=- n\dfrac{S\left( B_{2}-B_{1} \right)}{t_{2}-t_{1}}$；

故选：$\rm C$；

（不定项）如图所示，两条相同的半圆弧形光滑金属导轨固定在水平桌面上，其所在平面竖直且平行，导轨最高点到水平桌面的距离等于半径，最低点的连线$OO'$与导轨所在竖直面垂直。空间充满竖直向下的匀强磁场（图中未画出），导轨左端由导线连接。现将具有一定质量和电阻的金属棒$MN$平行$OO'$放置在导轨图示位置，由静止释放。$MN$运动过程中始终平行于$OO'$且与两导轨接触良好，不考虑自感影响，下列说法正确的是$(\qquad)$

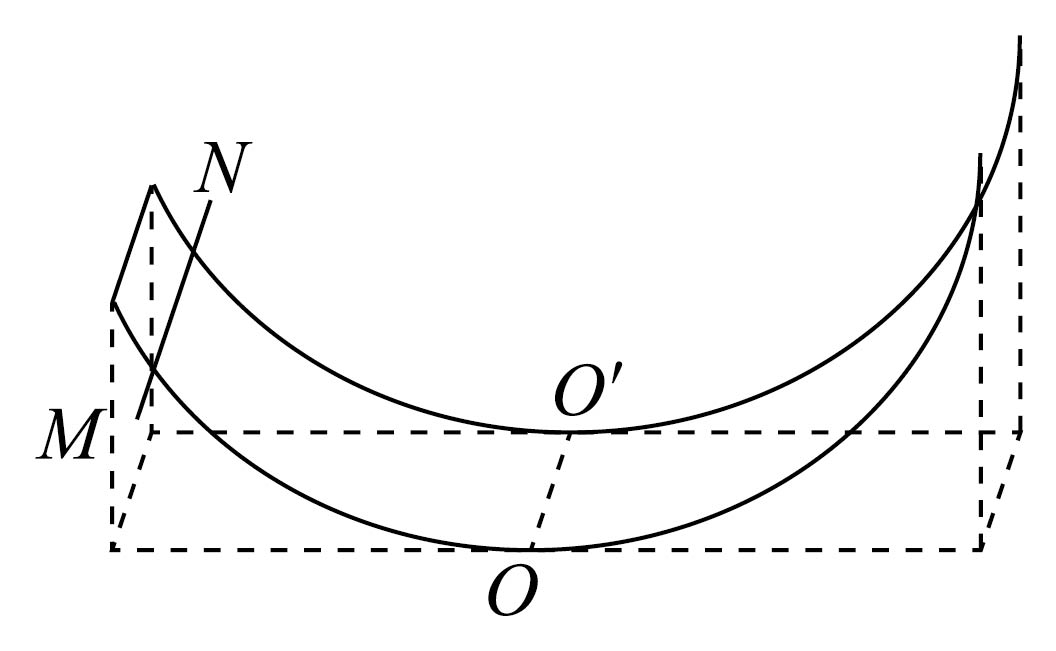
$MN$最终一定静止于$OO'$位置

$MN$运动过程中安培力始终做负功

从释放到第一次到达$OO'$位置过程中，$MN$的速率一直在增大

从释放到第一次到达$OO'$位置过程中，$MN$中电流方向由$M$到$N$

$\rm A$．由于金属棒$MN$运动过程切割磁感线产生感应电动势，回路有感应电流，产生焦耳热，金属棒$MN$的机械能不断减小，由于金属导轨光滑，所以经过多次往返运动，$MN$最终一定静止于$OO'$位置，故$\rm A$正确；

$\rm B$．当金属棒$MN$向右运动，根据右手定则可知，$MN$中电流方向由$M$到$N$，根据左手定则，可知金属棒$MN$受到的安培力水平向左，则安培力做负功；当金属棒$MN$向左运动，根据右手定则可知，$MN$中电流方向由$N$到$M$，根据左手定则，可知金属棒$MN$受到的安培力水平向右，则安培力做负功；可知$MN$运动过程中安培力始终做负功，故$\rm B$正确；

$\rm C$．金属棒$MN$从释放到第一次到达$OO'$位置过程中，由于在$OO'$位置重力沿切线方向的分力为$0$，可知在到达$OO'$位置之前的位置，重力沿切线方向的分力已经小于安培力沿切线方向的分力，金属棒$MN$已经做减速运动，故$\rm C$错误；

$\rm D$．从释放到第一次到达$OO'$位置过程中，根据右手定则可知，$MN$中电流方向由$M$到$N$，故$\rm D$正确。

故选：$\rm ABD$；

如图甲所示，不计电阻的平行金属导轨与水平面成$37^\circ$，导轨间距为$L=1\;\rm m$，上端接有电阻$R=3\;\rm \Omega$，虚线$OO'$下方是垂直于导轨平面的匀强磁场。现将质量$m=0.1\;\rm kg$、电阻$r=1\;\rm \Omega$的金属杆$ab$从$OO'$上方某处垂直导轨由静止释放，杆下落过程中始终与导轨保持良好接触，杆下落过程中的$v − t$图像如图乙所示。$g$取$10\;\rm m/s^{2}$。

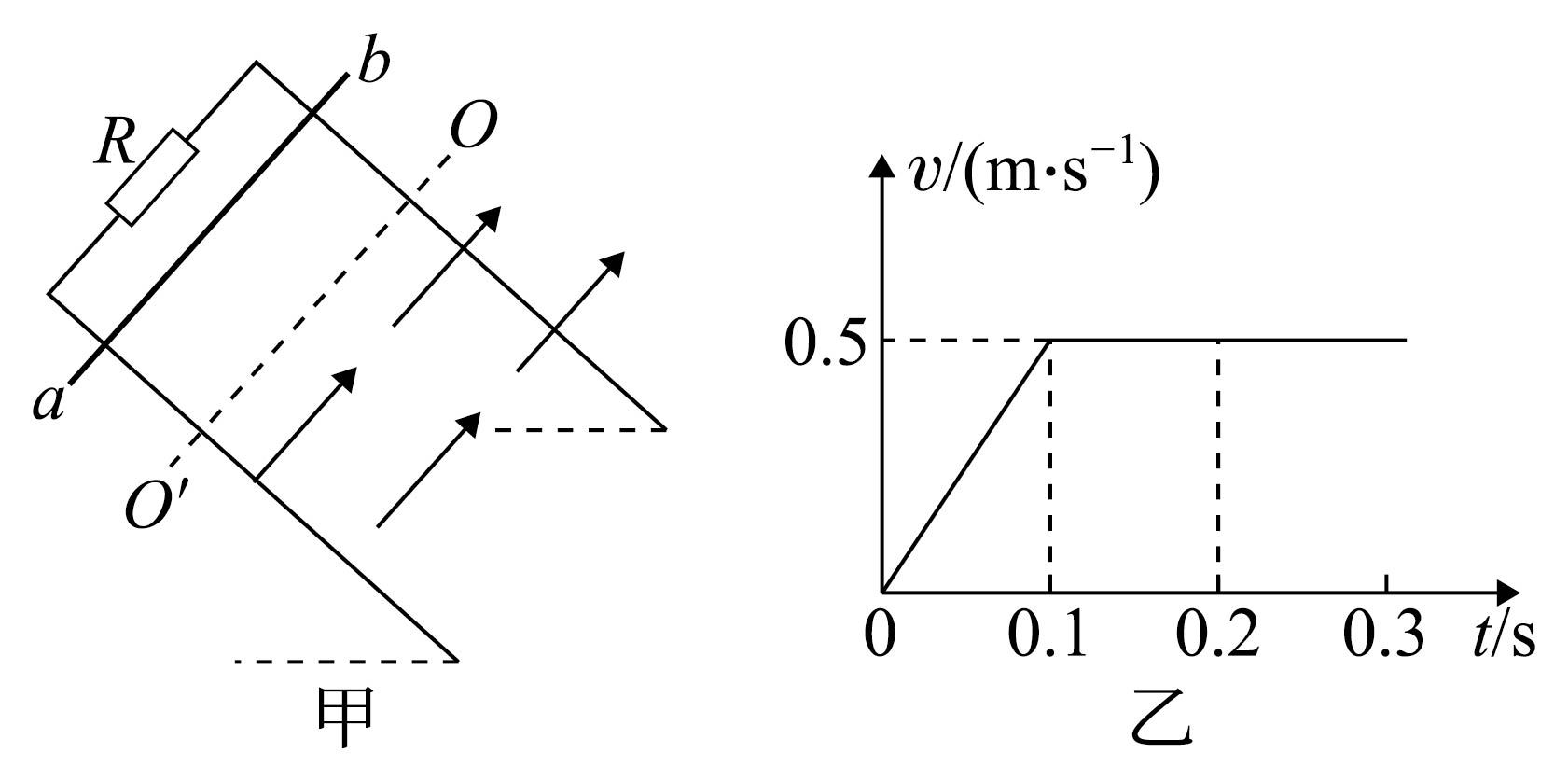
①金属杆在磁场中运动时，                 点电势高；（选填“$a$”或“$b$”）

②（计算）求磁感应强度$B$的大小                 ；

③杆在磁场中下滑$0.1\;\rm s$过程中，电阻$R$产生的焦耳热$Q_{R}=$                 $\;\rm J$。

①金属杆在磁场中运动时，根据右手定则可知，感应电流由$b→a$，等效电源内部由低电势流向高电势，即$a$点点电势高；

②由图乙得$a=\dfrac{\Delta v}{\Delta t}=\dfrac{0.5}{0.1}\text{m}/\text{s}^{2}=5\;\rm \text{m}/\text{s}^{2}$，$0.1\ \rm s$前，由牛顿第二定律有$mg\sin$ $\theta-f=ma$，代入数据得$f=0.1\;\rm N$，$0.1\;\rm s$后匀速运动，有$mg\sin$ $\theta-f-F_{A}=0$，而$F_{A}=BIL=$$B \cdot \dfrac{BLv}{R+r} \cdot L=\dfrac{B^{2}L^{2}v}{R+r}$，联立解得$B=2\;\rm T$；

③杆在磁场中下滑$0.1\ \rm s$过程中的电流$I=\dfrac{BLv}{R+r}=\dfrac{2 \times 1 \times 0.5}{3+1}{\;\rm A=0.25\;\rm A}$

电阻$R$产生的热量$Q=I^{2}Rt=0.25^{2} \times 3 \times 0.1\;\rm J=1.875 \times 10^{-2}\;\rm J$。