高中 | 闭合电路的欧姆定律基本问题 题目答案及解析
稿件来源:高途
高中 | 闭合电路的欧姆定律基本问题题目答案及解析如下,仅供参考!
选修3-1
第二章 恒定电流
2.7 闭合电路的欧姆定律
闭合电路的欧姆定律基本问题
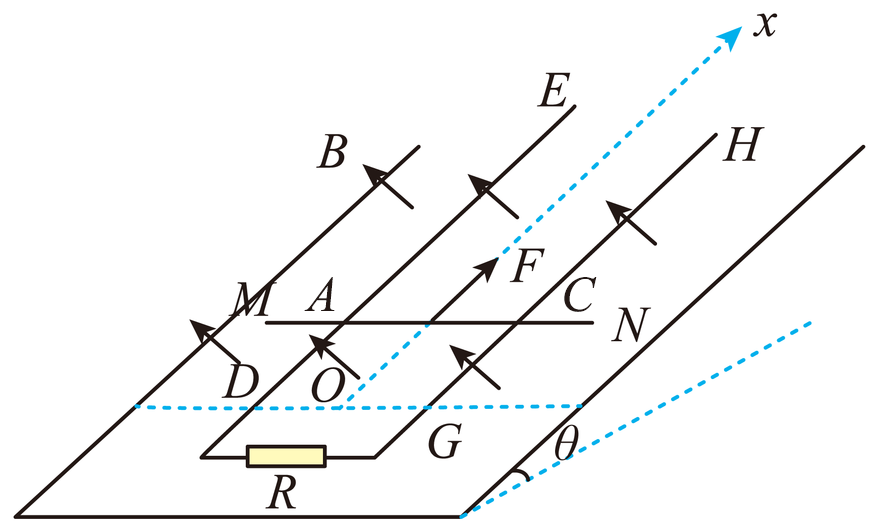
如图所示,在倾角$\theta=37^{∘}$的绝缘斜面上固定着两条粗细均匀且相互平行的光滑金属导轨$DE$和$GH$,间距$d=1\;\rm m$,每条金属导轨单位长度的电阻$r_{0}=0.5\;\rm \Omega/m$,$DG$水平,且$DG$两端点接了一个阻值$R=2\;\rm \Omega$的电阻。以$DG$中点$O$为坐标原点,沿斜面向上平行于$GH$方向建立$x$轴,在$DG$连线沿斜面向上的整个空间存在着垂直于斜面向上的磁场,且磁感应强度大小$B$与坐标$x$满足关系$B=(0.6+0.2x)\;\rm T$,一根长$L=2\;\rm m$,电阻$r=2\;\rm \Omega$,质量$m=0.1\;\rm kg$的粗细均匀的金属棒$MN$平行于$DG$放置,在拉力$F$作用下以恒定的速度$v=1\;\rm m/s$从$x=0$处沿$x$轴正方向运动,金属棒与两导轨接触良好。$\sin 37^{∘} =0.6$,$\cos 37^{∘} =0.8$,计其它电阻。求
金属棒上的电流方向;(选答“$A$向$C$”或“$C$向$A$”)
$A$向$C$
"]]由右手定则可以判定导体棒中电流的方向为$A$向$C$。
金属棒通过$x=2\;\rm m$处时,流过$R$的电流大小;
$0.2\\;\\rm A$
"]]金属棒连入电路部分产生的感应电动势为$E_{1}=B_{1}dv=(0.6+0.2 \times 2) \times 1 \times 1\;\rm V=1\;\rm V$
根据闭合电路欧姆定律可得电流大小$I_{1}=\dfrac{E_{1}}{R+\dfrac{d}{l}r+2xr_{0}}=0.2\;\rm \text{A}$。
金属棒通过$x=2\;\rm m$处时,棒两端的电势差$U_{MN}$;
$-0.18\\;\\rm V$
"]]由右手定则知$M$点电势低于$N$点电势,根据欧姆定律可得金属棒通过$x=2m$处时两端的电势差$U_{MN}=−[I_{1}(R+2xr_{0})+B_{1}(l − d)]v=-1.8\;\rm V$。
金属棒从$x=0$到$x=3\;\rm m$过程中,$R$上产生的热量和外力$F$做的功。
$0.24$;$2.34\\;\\rm J$
"]]金属棒做匀速直线运动$I=\dfrac{Bdv}{R+\dfrac{d}{l}r+2xr_{0}}=\dfrac{(0.6+0.2x) \times 1 \times 1}{3+x}\text{A}=0.2\;\rm \text{A}$
$t=\dfrac{x}{v}=3\;\rm \text{s}$,$R$上产生的热量$Q=I^{2}Rt=0.24\;\rm J$
金属棒做匀速直线运动,则有$F=mg\sin \theta+BdI$
此过程$F$随位移均匀变化$F=0.72+0.04x$
金属棒从$x=0$到$x=3\;\rm m$过程中,外力$F$做的功$W=\overline{F}x=\dfrac{0.72+0.84}{2} \times 3\;\rm \text{J}=2.34\;\rm \text{J}$。
高中 | 闭合电路的欧姆定律基本问题题目答案及解析(完整版)
