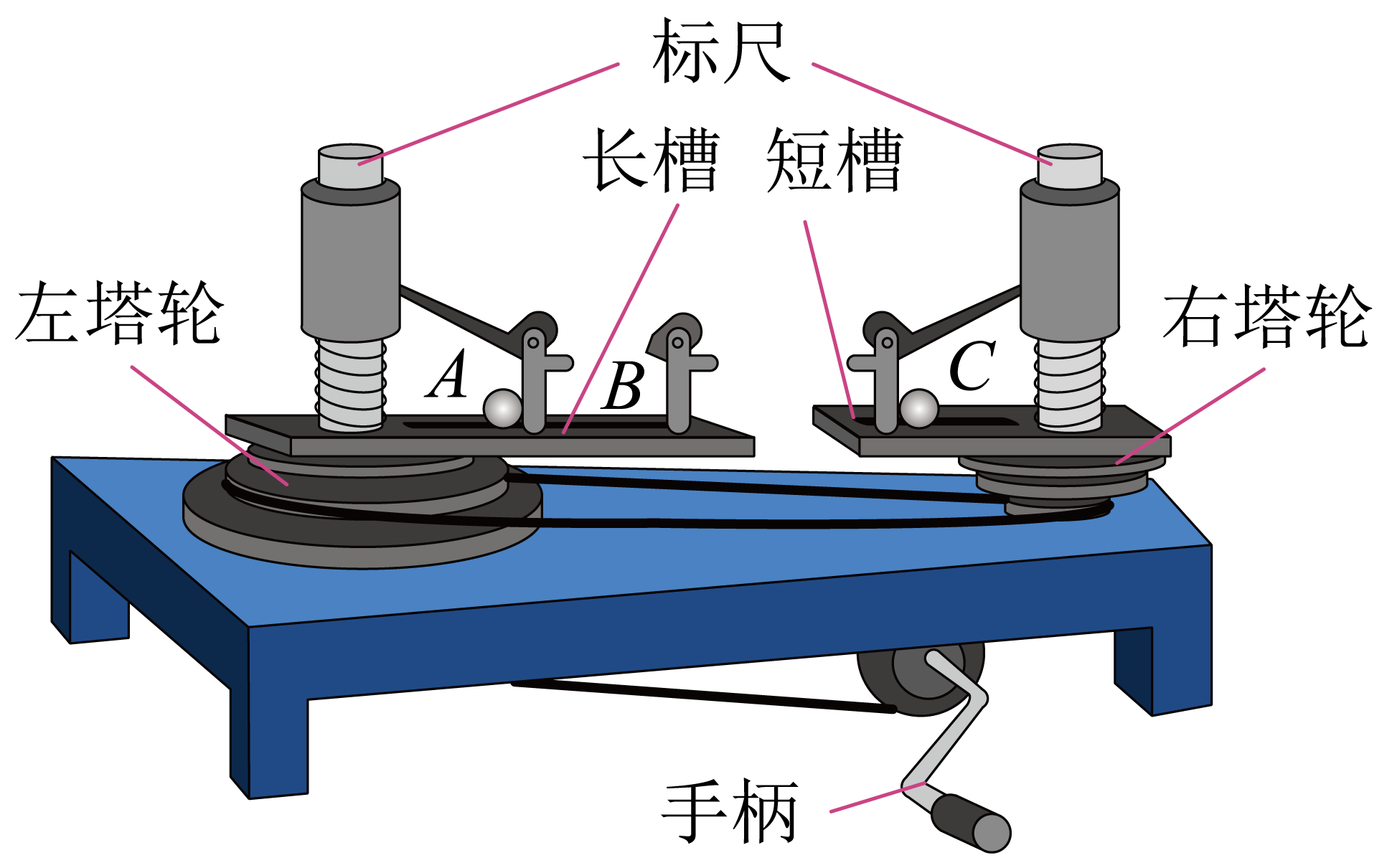
在探究向心力与半径、质量、角速度的关系时，用到的实验方法是$(\quad\ \ \ \ )$。（填正确答案标号）

微元法

等效替代法

控制变量法

理想化模型法

在探究向心力大小$F$与半径$r$、质量$m$、角速度$\omega$的关系时，需要先控制某些量不变，探究其中的两个物理量的关系，即用控制变量法。

故选：$\rm C$。

在某次实验中，某同学把两个质量相等的钢球放在$A$、$C$位置，$A$、$C$到塔轮中心距离相同，将皮带处于左右塔轮的半径不等的层上，匀速转动手柄，观察左右标尺露出的刻度，左边标尺露出$1$格，右边标尺露出$4$格，则皮带连接的左、右塔轮半径之比为                 。

由$F=m\omega^{2}r$

可知，两球的向心力之比为$1:4$，两球的质量相等，转动半径相同，则有转动的角速度之比为$1:2$，因用皮带连接的左、右塔轮，轮缘的线速度大小相等，由$v=\omega r$

可知，左、右塔轮半径之比为$2:1$。

在（$2$）的实验中，其他条件不变，若减小手柄匀速转动的速度，则下列符合实验实际的是$(\quad\ \ \ \ )$。（填正确答案标号）

左右两标尺的示数将变大，两标尺示数的比值变大

左右两标尺的示数将变大，两标尺示数的比值变小

左右两标尺的示数将变小，两标尺示数的比值变小

左右两标尺的示数将变小，两标尺示数的比值不变

其他条件不变，若减小手柄转动的速度，则有两钢球所需的向心力都减小，左右两标尺的示数将变小，可是向心力之比不变，即两标尺示数的比值不变。

故选：$\rm D$。