高中 | 探究向心力大小与半径、角速度、质量的关系 题目答案及解析
稿件来源:高途
高中 | 探究向心力大小与半径、角速度、质量的关系题目答案及解析如下,仅供参考!
必修2
第五章 曲线运动
5.6 向心力
探究向心力大小与半径、角速度、质量的关系
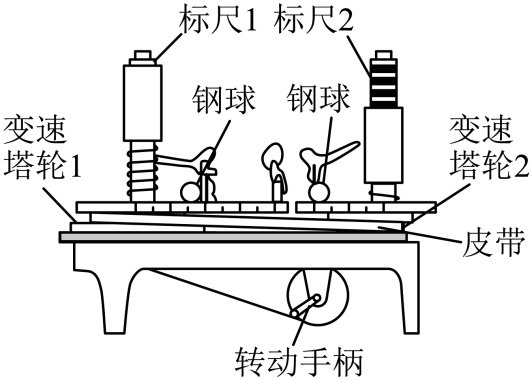
探究向心力大小$F$与小球质量$m$、角速度$\omega$和半径$r$之间关系的实验装置如图所示,转动手柄,可使变速塔轮、长槽和短槽随之匀速转动。皮带分别套在塔轮的圆盘上,可使两个槽内的小球分别以不同角速度做匀速圆周运动。小球做圆周运动的向心力由横臂的挡板提供,同时,小球对挡板的弹力使弹簧测力筒下降,从而露出测力筒内的标尺,标尺上露出的红白相间的等分格数之比即为两个小球所受向心力的比值。
在这个实验中,利用了 (选填“理想实验法”“等效替代法”或“控制变量法”)来探究向心力的大小与小球质量$m$、角速度$\omega$和半径$r$之间的关系;
在这个实验中,利用了控制变量法来探究向心力的大小与小球质量$m$、角速度$\omega$和半径$r$之间的关系;
探究向心力的大小与圆周运动半径的关系时,应选择两个质量 (选填“相同”或“不同”)的小球;
探究向心力的大小与圆周运动半径的关系时,应选择两个质量相同的小球;
探究向心力的大小与圆周运动的角速度的关系,左右两边塔轮的半径 (选填“相同”或“不同”)
探究向心力的大小与圆周运动的角速度的关系,左右两边塔轮的半径不同,根据$v=r\omega$
可知此时角速度不同;
当用两个质量相等的小球做实验,调整长槽中小球的轨道半径等于短槽中小球的轨道半径,转动时发现左、右标尺上露出的红白相间的等分格数之比为$4:1$,则左、右两边塔轮的半径之比为 。
根据$F=m\omega^{2}R$
由题意可知
可得$\omega_{左}:\omega_{右}=2:1$
由$v=\omega r$
可得$r_{左}:r_{右}=1:2$
左、右两边塔轮的半径之比是$1:2$。
高中 | 探究向心力大小与半径、角速度、质量的关系题目答案及解析(完整版)
