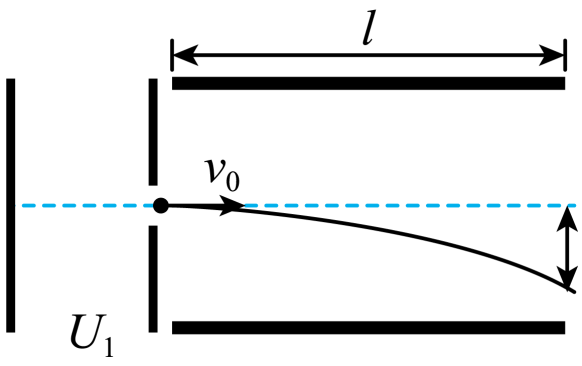
电子进入偏转电场时的速度；

$4\\times10^{7}\\;\\rm m/s$

设电子经加速电场$U_{1}$加速后以速度$v_{0}$进入偏转电场，由动能定理有$qU_{1}=\dfrac{1}{2}m{v_{0}}^{2}$

则有$v_{0}=\sqrt{\dfrac{2qU_{1}}{m}}=4 \times 10^{7}\;{\text{m}}/{\text{s}}$

射出偏转电场时速度的偏角$\tan \theta$；

$\\tan\\theta=\\dfrac{1}{10}$

电子进入偏转电场的速度$v_{0}=4\times10^{7}\;\rm m/s$

进入偏转电场后在电场线方向有$a=\dfrac{qU_{2}}{md}$

经时间$t_{1}$飞出电场有$t_{1}=\dfrac{l}{v_{0}}$

以上各式联立解得射出偏转电场时在竖直方向上的速度为$v_{{y}}=at_{1}=\dfrac{qU_{2}l}{mdv_{0}}=4 \times 10^{6}\;\rm \text{m/s}$

设射出偏转电场时速度的偏角为$\theta$，则$\tan\theta=\dfrac{v_{{y}}}{v_{\text{0}}}=\dfrac{1}{10}$

电子在偏转电场方向的位移。

$0.25\\;\\rm cm$

飞出电场时偏转量为$y_{1}=\dfrac{1}{2}a{t_{1}}^{2}$

由以上各式得$y_{1}=\dfrac{U_{2}l^{2}}{4dU_{1}}=0.25\;\rm \text{cm}$