| 示波管 题目答案及解析
稿件来源:高途
| 示波管题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
示波管
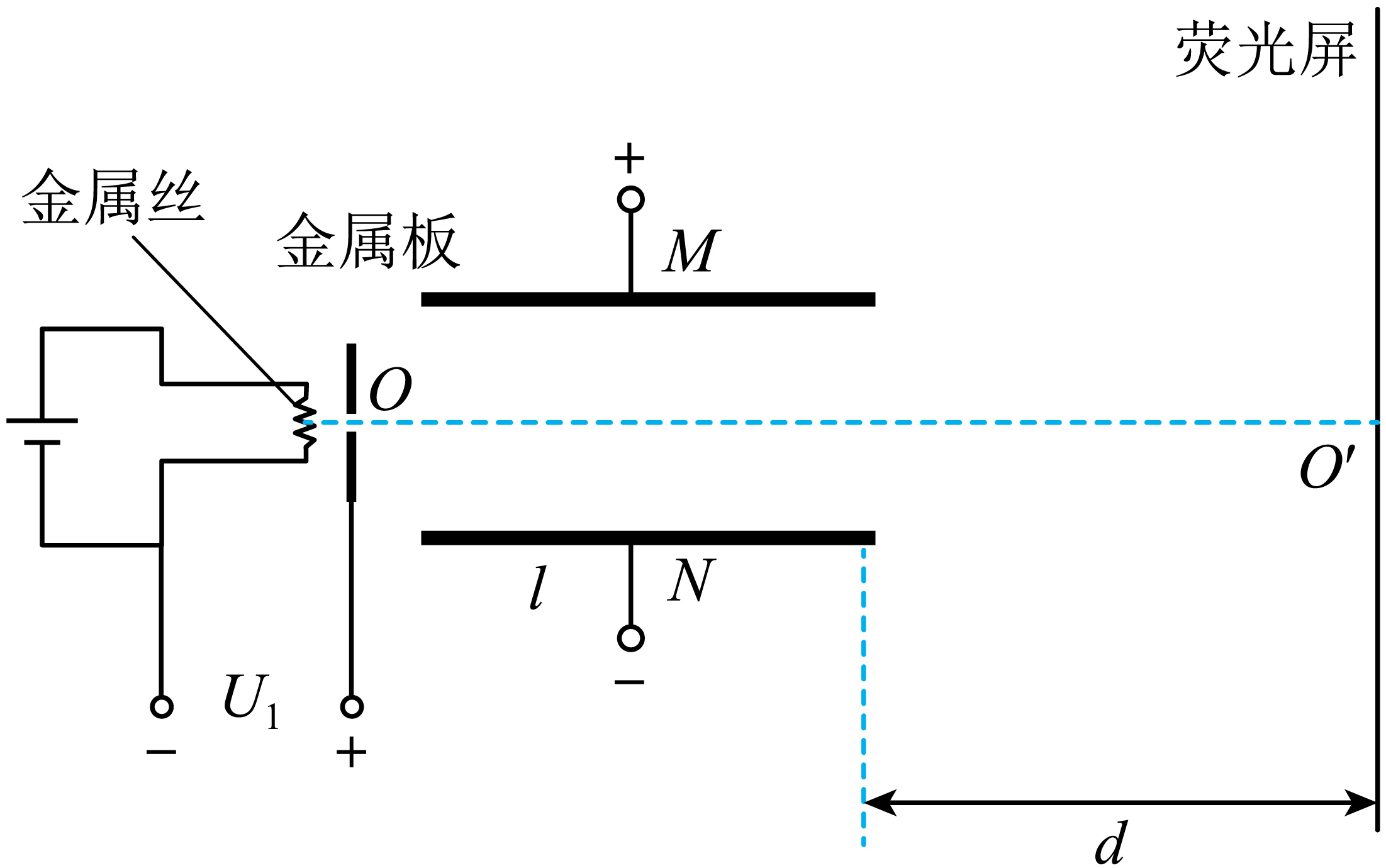
如图所示,示波器的工作原理可以简化为:金属丝发射出的电子由静止经电压$U_{1}$加速后,从金属板的小孔$O$射出,沿$OO'$进入偏转电场,经偏转电场后打在荧光屏上。偏转电场是由两个平行的相同金属极板$M$、$N$组成,已知极板的长度为$l$,两板间的距离也为$l$。极板间电压为$U_{2}$,偏转电场极板的右端到荧光屏的距离为$d$。电子电荷量大小为$e$,质量为$m$,不计电子受到的重力和电子之间的相互作用。
求电子从小孔$O$穿出时的速度大小$v_{0}$:
$\\sqrt{\\dfrac{2eU_{1}}{m}}$;
"]]电子在加速电场做加速运动,根据动能定理可得$eU_{1}=\dfrac{1}{2}mv_{0}^{2}$
解得$v_{0}=\sqrt{\dfrac{2eU_{1}}{m}}$
求电子离开偏转电场时速度偏转角度的正切值和在荧光屏上形成的亮斑到$O$的距离。
$\\dfrac{U_{2}}{2U_{1}}$,$\\dfrac{U_{2}(l+2d)}{4U_{1}}$
"]]在偏转电场中,水平方向电子做匀速运动,有$l=v_{0}t$
竖直方向,电子受到电场力作用,由牛顿第二定律有$e\dfrac{U_{2}}{l}=ma$
又$y=\dfrac{1}{2}at^{2}$,$v_{y}=at$,$\tan\theta=\dfrac{v_{y}}{v_{0}}$
联立解得电子离开偏转电场时速度偏转角度的正切值为$\tan\theta=\dfrac{U_{2}}{2U_{1}}$
根据类平抛推论和几何关系可得$y'=\dfrac{\dfrac{l}{2}+d}{\dfrac{l}{2}}y$
联立解得在荧光屏上形成的亮斑到$O$的距离为$y'=\dfrac{U_{2}(l+2d)}{4U_{1}}$
| 示波管题目答案及解析(完整版)
