高中 | 力的分解 题目答案及解析
稿件来源:高途
高中 | 力的分解题目答案及解析如下,仅供参考!
必修1
第三章 相互作用
3.5 力的分解
力的分解
($2025·$山东$·$模拟预测)学校组织趣味运动会,某运动员手持乒乓球拍托着球沿水平直赛道向前跑,运动员速度越大,乒乓球受到的水平风力越大。已知球拍面与水平面的夹角为$30^\circ$,乒乓球的质量为$3\;\rm g$,乒乓球与球拍面之间的动摩擦因数为$\dfrac{\sqrt{3}}{4}$,最大静摩擦力等于滑动摩擦力,取$g=10\;\rm m/s^{2}$,不考虑乒乓球的滚动,当运动员以某一速度匀速向前跑时,乒乓球恰好不上滑,则下列说法正确的是$(\qquad)$
乒乓球受三个力的作用
","乒乓球受到的摩擦力方向沿球拍向上
","乒乓球受到的风力大小为$\\dfrac{7\\sqrt{3}}{3} \\times 10^{- 2}\\;\\rm \\text{N}$
","如果球拍面竖直,则乒乓球一定会下滑
"]$\rm B$.乒乓球恰好不上滑,所以乒乓球有沿球拍上滑的趋势,乒乓球受沿球拍面向下的摩擦力,$\rm B$错误;
$\rm A$.对乒乓球受力分析如图所示,乒乓球受重力、球拍支持力、球拍的摩擦力和水平风力共四个力的作用,$\rm A$错误;
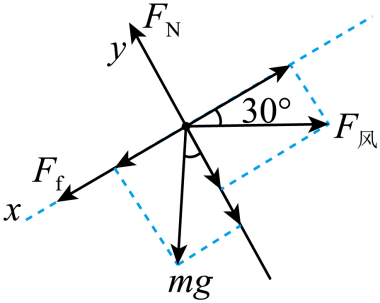
$\rm C$.对乒乓球受力分析并正交分解,$x$轴方向有
$\mu F_{N}+mg\sin 30^\circ-F_{风}\cos 30^\circ =0$
$y$轴方向有$F_{N}-mg\cos 30^\circ-F_{风}\sin 30^\circ =0$
联立解得$F_{\text{风}}=\dfrac{7\sqrt{3}}{3} \times 10^{-2}\;\rm \text{N}$
$\rm C$正确;
$\rm D$.当球拍竖直时,如果水平风力足够大,能使乒乓球受到的静摩擦力等于重力,乒乓球就不会下滑,$\rm D$错误。
故选:$\rm C$。
高中 | 力的分解题目答案及解析(完整版)
